
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
分析 通过数列a1,a2,…,a670的“平均和”为2013,可知S1+S2+…S670=2013×670,T671=4+$\frac{1}{671}$(S1+S2+…S670)代值即可
解答 解:∵数列a1,a2,…,a670的“平均和”为2013,
∴T670=$\frac{{S}_{1}+{S}_{2}+{S}_{3}+…+{S}_{670}}{670}$=2013,
∴S1+S2+…S670=2013×670,
∴4,a1,a2,…,a670的“平均和”
T671=$\frac{4+(4+{S}_{1})+(4+{S}_{2})+…+(4+{S}_{670})}{671}$
=4+$\frac{1}{671}$(S1+S2+…S670)
=4+$\frac{2013×670}{671}$
=4+3×670
=2014,
故选:C.
点评 本题考查了数列新定义的求和问题的应用,解题时须认真分析,从题目中寻找解答问题的关键,从而得出答案,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.001的前提下,认为“数学成绩与物理成绩有关” | |
| B. | 在犯错误的概率不超过0.01的前提下,认为“数学成绩与物理成绩有关” | |
| C. | 有99%以上的把握认为“数学成绩与物理成绩无关” | |
| D. | 有99.9%以上的把握认为“数学成绩与物理成绩有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2{e^2}}}$ | B. | $\frac{1}{2}{e^2}$ | C. | $\frac{1}{e}$ | D. | $-\frac{3}{{2{e^2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
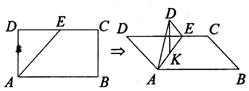 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com