
【题目】已知![]() (
(![]() 且m为常数).
且m为常数).
(1)讨论函数![]() 的单调性;
的单调性;
(2)若对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() (其中e为自然对数的底数),求实数k的取值范围.
(其中e为自然对数的底数),求实数k的取值范围.
【答案】(1)当![]() 时,
时,![]() 递增区间是
递增区间是![]() ,无递减区间,当
,无递减区间,当![]() 时,
时,![]() 递增区间是
递增区间是![]() ,递减区间是
,递减区间是![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() ,对
,对![]() 分类讨论,求出
分类讨论,求出![]() 的解,就可得出结论;
的解,就可得出结论;
(2)设![]() ,所求的问题转化为
,所求的问题转化为![]() ,通过求导数法,求出
,通过求导数法,求出![]() 取最大值时自变量
取最大值时自变量![]() 与
与![]() 的关系,而对任意的
的关系,而对任意的![]() 都成立,将
都成立,将![]() 用
用![]() 表示,构造新函数,再求导求出新函数的最小值,即可求出结论.
表示,构造新函数,再求导求出新函数的最小值,即可求出结论.
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,当
,当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,
,
综上,当![]() 时,
时,![]() 递增区间是
递增区间是![]() ,无递减区间,
,无递减区间,
当![]() 时,
时,![]() 递增区间是
递增区间是![]() ,递减区间是
,递减区间是![]() ;
;
(2)设![]() ,依题意
,依题意![]() ,
,
![]() ,令
,令![]() ,
,
![]() 恒成立,
恒成立,![]() 在
在![]() 是减函数,
是减函数,
即![]() 在
在![]() 是减函数,
是减函数,![]() ,
,
![]() ,存在唯一
,存在唯一![]() ,使得
,使得![]() ,
,
当![]() ,
,
![]() 递增区间是
递增区间是![]() ,递减区间是
,递减区间是![]() ,
,
![]() 取得极大值,也是最大值为
取得极大值,也是最大值为![]() ,
,
![]() ,
,
对于对任意的![]() 恒成立,
恒成立,
其中![]() ,
,![]() ,
,
即![]() ,
,
对于对任意的![]() 恒成立,
恒成立,
设![]() ,
,
![]() ,
,
![]()
![]() 时,
时,![]() ,
,
![]() ,当
,当![]() ,
,
![]() 时,
时,![]() 取得极小值,也是最小值,
取得极小值,也是最小值,
即![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在![]() 内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:

(1)算出第三组![]() 的频数.并补全频率分布直方图;
的频数.并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,数列
,数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若对任意正整数![]() ,不等式
,不等式![]() 均成立,求
均成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,焦距为2c,圆
,焦距为2c,圆![]() ,
,![]() ,
,![]() 是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形
是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形![]() 面积的最大值为
面积的最大值为![]() .
.

(1)求椭圆C的方程;
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于M,N两点,直线
与圆O相切,且与椭圆相交于M,N两点,直线![]() 与
与![]() 平行且与椭圆相切于P(O,P两点位于
平行且与椭圆相切于P(O,P两点位于![]() 的同侧),求直线
的同侧),求直线![]() ,
,![]() 距离d的取值范围.
距离d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,焦距为2c,圆
,焦距为2c,圆![]() ,
,![]() ,
,![]() 是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形
是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形![]() 面积的最大值为
面积的最大值为![]() .
.
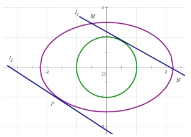
(1)求椭圆C的方程;
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于M,N两点,直线
与圆O相切,且与椭圆相交于M,N两点,直线![]() 与
与![]() 平行且与椭圆相切于P(O,P两点位于
平行且与椭圆相切于P(O,P两点位于![]() 的同侧),求直线
的同侧),求直线![]() ,
,![]() 距离d的取值范围.
距离d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 到点
到点![]() 的距离比它到直线
的距离比它到直线![]() 距离小
距离小![]()
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,它们与(Ⅰ)中轨迹
,它们与(Ⅰ)中轨迹![]() 分别交于点
分别交于点![]() 及点
及点![]() ,且
,且![]() 分别是线段
分别是线段![]() 的中点,求
的中点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有四个关于命题的判断,其中正确的是()
A.命题“![]() ,
,![]() ”是假命题
”是假命题
B.命题“若![]() ,则
,则![]() 或
或![]() ”是真命题
”是真命题
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是钝角三角形”是真命题
是钝角三角形”是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com