
| A. | [-$\frac{1}{2}$,1] | B. | (-∞,0)∪[1,+∞) | C. | (-$\frac{1}{2}$,1] | D. | (-∞,0]∪[1,+∞) |
分析 首先由由f(x)的图象关于(0,0)中心对称,可得f(x)为奇函数,根据不等式f(s2-2s)≤-f(2t-t2),其中t=k•s,得出s与t的关系式,然后利用线性规划的知识,数形结合即可求得结果.
解答 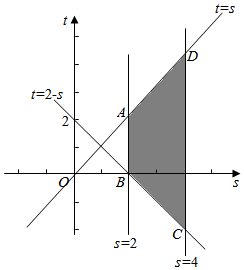 解:定义在R上的函数f(x)是减函数,且函数y=f(x)的图象关于原点中心对称,
解:定义在R上的函数f(x)是减函数,且函数y=f(x)的图象关于原点中心对称,
故f(x)为奇函数.
若s,t满足不等式f(s2-2s)≤-f(2t-t2),其中t=k•s,2<s<4.
则f(s2-2s)≤f(-2t+t2),s2-2s>-2t+t2 ,求得2-s≤t≤s.
∵k=$\frac{t}{s}$=$\frac{t-0}{s-0}$ 表示图中四边形ABCD及其内部区域内的点与原点O连线的斜率,
故当点(s,t)位于线段AD上时,k取得最大值为1;
当点(s,t)位于点D(4,-2)时,k取得最小值为-$\frac{1}{2}$.
故k的取值范围为[-$\frac{1}{2}$,1],
故选:C.
点评 本题综合考查函数的奇偶性、单调性知识,同时考查由最大值、最小值求取值范围的策略,以及运算能力,属中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 茎叶图 | B. | 分层抽样 | C. | 独立性检验 | D. | 回归直线方程 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 | B. | 30 | C. | 31 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos20° | B. | sin20° | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (-∞,1) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com