
 中,
中,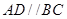 ,
,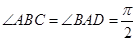 ,
,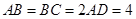 ,
,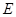 、
、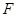 分别是
分别是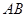 、
、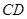 上的动点,且
上的动点,且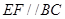 ,设
,设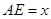 (
(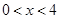 )。沿
)。沿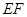 将梯形
将梯形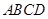 翻折,使平面
翻折,使平面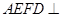 平面
平面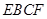 ,如图(2)。
,如图(2)。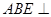 平面
平面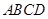 ;
;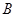 、
、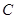 、
、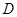 、
、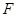 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为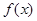 ,求
,求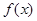 的最大值;
的最大值;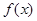 取得最大值时,求二面角
取得最大值时,求二面角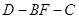 的正弦值.
的正弦值.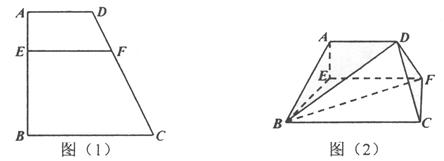
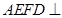 平面
平面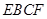 ,
,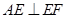 ,∴
,∴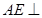 平面
平面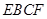 ,
,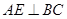
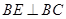 , 又
, 又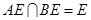
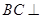 平面
平面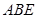 。
。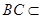 平面
平面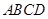 ,
,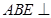 平面
平面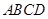 . ………………4分
. ………………4分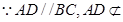 平面
平面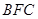 ,
,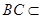 平面
平面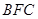 ,
,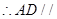 平面
平面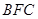 .
.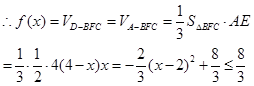 ……………………………………6分
……………………………………6分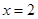 时,
时,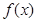 有最大值
有最大值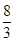 . ……………………………………8分
. ……………………………………8分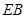 、
、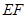 、
、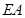 为轴建立空间直角坐标系,
为轴建立空间直角坐标系,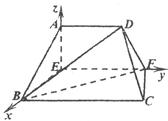 则
则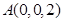 ,
,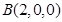 ,
,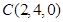 ,
,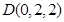 ,
,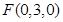
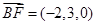 ,
,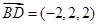 ,
,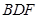 的法向量为
的法向量为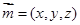 ,
,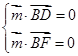 ∴
∴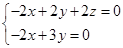
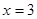 ,则
,则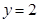 ,
,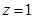 ,∴
,∴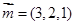 ……………………………10分
……………………………10分 的一个法向量为
的一个法向量为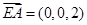 ,
,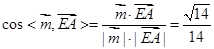 , ……………………………12分
, ……………………………12分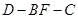 为
为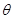 ,∴
,∴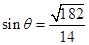
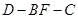 的正弦值为
的正弦值为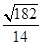 …………………………………14分
…………………………………14分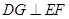 于
于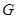 ,作
,作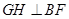 于
于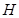 ,连
,连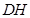 。由(1)知平面
。由(1)知平面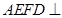 平面
平面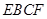 ,
,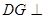 平面
平面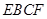
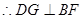 又
又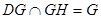
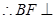 平面DGH
平面DGH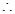
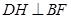
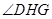 是二面角
是二面角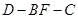 的平面角的补角.…………………………………10分
的平面角的补角.…………………………………10分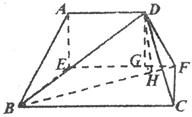 由
由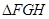 ∽
∽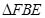 ,知
,知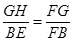 ,
,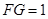 ,
,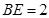 ,
,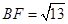 ,
,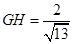
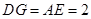 ,∴
,∴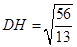 ……………12分
……………12分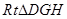 中,
中,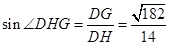 。
。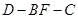 的正弦值为
的正弦值为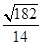 …………………………………14分
…………………………………14分 

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
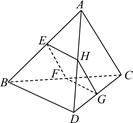
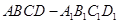 中,E,P分别是侧棱B1C1,
中,E,P分别是侧棱B1C1,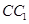 上的中点
上的中点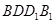 所成角的正切值
所成角的正切值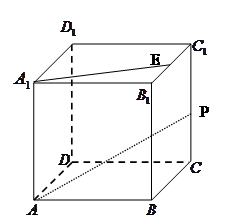
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
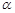 的一个充分条件是( )
的一个充分条件是( )A.存在一条直线b,b∥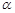 ,a∥b ,a∥b |
B.存在一个平面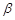 , ,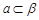 , ,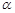 ∥ ∥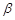 |
C.存在一个平面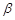 ,a∥ ,a∥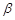 , ,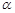 ∥ ∥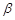 |
D.存在一条直线b,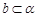 ,a∥b ,a∥b |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
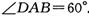 ,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.
,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.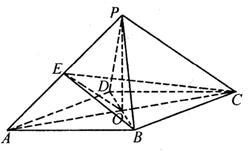
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com