
分析 假设存在常数a,b,使等式对于一切n∈N*都成立.取n=1,2可得a,b的值,再用数学归纳法证明,数学归纳法的一般步骤是,第一步验证第一项是否成立,第二步假设n=k时候结论成立,去验证n=k+1时候结论是否成立.若都成立即得证.
解答 解:若存在常数a,b,使等式对于一切n∈N*都成立.
取n=1,2可得$\left\{\begin{array}{l}{\frac{1}{3}=\frac{a+1}{b+2}}\\{\frac{1}{3}+\frac{4}{15}=\frac{4a+2}{2b+2}}\end{array}\right.$,解得a=1,b=4.
则$\frac{{1}^{2}}{1×3}$+$\frac{{2}^{2}}{3×5}$+…+$\frac{{n}^{2}}{(2n-1)(2n+1)}$=$\frac{{n}^{2}+n}{4n+2}$对于一切n∈N*都成立.
下面用数学归纳法证明:
(1)当n=1时,显然成立.
(2)假设当n=k(k∈N*)时,等式成立,即$\frac{{1}^{2}}{1×3}$+$\frac{{2}^{2}}{3×5}$+…+$\frac{{k}^{2}}{(2k-1)(2k+1)}$=$\frac{{k}^{2}+k}{4k+2}$对于一切n∈N*都成立.
则当n=k+1时,$\frac{{1}^{2}}{1×3}$+$\frac{{2}^{2}}{3×5}$+…+$\frac{{k}^{2}}{(2k-1)(2k+1)}$+$\frac{(k+1)^{2}}{(2k+1)(2k+3)}$=$\frac{{k}^{2}+k}{4k+2}$+$\frac{(k+1)^{2}}{(2k+1)(2k+3)}$,
=(k+1)•$\frac{k(2k+3)+2(k+1)}{2(k+1)(2k+3)}$,
=(k+1)•$\frac{(2k+1)(k+2)}{2(2k+1)(2k+3)}$,
=$\frac{(k+1)(k+2)}{2(2k+3)}$,
=$\frac{(k+1)^{2}+(k+1)}{4(k+1)+2}$.
也就是说当n=k+1时,等式也成立.
综上所述:可知等式对于一切n∈N*都成立.
点评 本题考查归纳推理的应用,着重考查数学归纳法,考查运算推理能力,属于中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
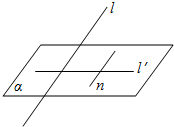 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-3,1) | C. | (3,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com