练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．数列{an}满足：an+2=an+1+an，且a1=a2=1，则a7=（　　）
    A．7B．8C．13D．21

    分析 利用递推关系即可得出．

    解答 解：∵an+2=an+1+an，且a1=a2=1，
    ∴a3=a1+a2=2，同理可得：a4=3，a5=5，a6=8，a7=13．
    故选：C．

    点评 本题考查了数列的递推关系，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

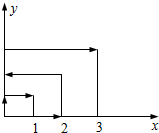    11．如图：一个质点在第一象限运动，在第一秒钟它由原点运动到点（0，1），而后接着按图所示在与x轴y轴平行的方向运动，且每秒移动一个单位长度，那么416秒后，这个质点所处的位置的坐标是（20，16）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．椭圆$\left\{{\begin{array}{l}{x=3cosϕ}\\{y=4sinϕ}\end{array}}$（ϕ为参数）的长轴长为（　　）
    A．3B．5C．6D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=x+$\frac{3}{x}$+2，（x≥$\sqrt{3}$）．
    ①判断函数y=f（x）在区间[$\sqrt{3}$，+∞）上的单调性，并加以证明．
    ②若函数g（x）=f（x）+x2-3x-$\frac{3}{x}$，且满足g（x）≥a恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数f（x）=2x|log0.5x|-1的零点个数为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知点A的极坐标为（2，$\frac{3π}{4}$），则它的直角坐标是（　　）
    A．（2，2）B．（1，$\frac{{\sqrt{2}}}{2}$ ）C．（-$\sqrt{2}$，$\sqrt{2}$）D．（$\sqrt{2}$，-$\sqrt{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

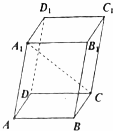    13．如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形，AB=4，AD=3，AA1=5，∠BAA1=∠DAA1=60°，则A1C的长为$\sqrt{85}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．命题“若x2＜9，则-3＜x＜3”的逆否命题是（　　）
    A．若x2≥9，则x≥3或x≤-3B．若-3＜x＜3，则x2＜9
    C．若x＞3或x＜-3，则x2＞9D．若x≥3或x≤-3，则x2≥9

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知复数z=$\frac{{{m^2}-m-6}}{m+3}$+（m2-2m-15）i
    （1）m取何实数值时，z是实数？
    （2）m取何实数值时，z是纯虚数？

    查看答案和解析>>

    同步练习册答案