
分析 ①函数y=f(x)在区间[$\sqrt{3}$,+∞)上单调递增,利用导数加以证明.
②若函数g(x)=f(x)+x2-3x-$\frac{3}{x}$,且满足g(x)≥a恒成立,则x2-2x+2≥a(x≥$\sqrt{3}$)恒成立,求出左边的最小值,即可求a的取值范围.
解答 解:①函数y=f(x)在区间[$\sqrt{3}$,+∞]上单调递增.
证明如下:∵f(x)=x+$\frac{3}{x}$+2,
∴f′(x)=1-$\frac{3}{{x}^{2}}$,
∵x≥$\sqrt{3}$,
∴f′(x)=1-$\frac{3}{{x}^{2}}$≥0,
∴函数y=f(x)在区间[$\sqrt{3}$,+∞)上单调递增.
②∵函数g(x)=f(x)+x2-3x-$\frac{3}{x}$,且满足g(x)≥a恒成立,
∴x2-2x+2≥a(x≥$\sqrt{3}$)恒成立,
∵x≥$\sqrt{3}$,∴x2-2x+2≥5-2$\sqrt{3}$,
∴a≤5-2$\sqrt{3}$.
点评 本题考查函数恒成立问题,考查导数知识的运用,考查函数的单调性,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3,4,5,6,7} | B. | {6} | C. | {2,4,5,6,7} | D. | {0,1,3,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y+1)2=1 | B. | x2+(y-1)2=1 | C. | (x-1)2+(y-1)2=1 | D. | x2+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
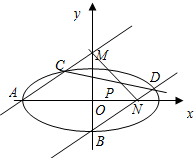 如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.
如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com