
分析 (1)由正弦定理,sin2B=2sinAsinC,转化成b2=2ac,由a=b,代入即可求得a=b=2c,根据余弦定理cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,代入即可求得cosB的值;
(2)由B=90°,根据勾股定理可知b2=a2+c2,由(1)可得b2=2ac,代入可求得a=c,由三角形面积公式S=$\frac{1}{2}$ac=1,求a.
解答 解:(1)在△ABC中由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=2R,
∵sin2B=2sinAsinC,
∴b2=2ac,
∵a=b,
∴a=b=2c,
由余弦定理可知:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{4}$,
cosB=$\frac{1}{4}$,
(2)B=90°,b2=a2+c2,
∵b2=2ac,
∴2ac=a2+c2,
∴a=c,
∵S=$\frac{1}{2}$ac=1,
∴a=$\sqrt{2}$.
点评 本题考查正弦定理及余弦定理的应用,考查勾股定理及三角形面积公式,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
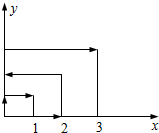 如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com