
分析 (1)求出函数的导数,求出切线方程,根据对应关系求出a,b的值即可;
(2)求出函数的导数,求出a的值,得到函数的单调区间,从而求出函数的最大值即可.
解答 解:(1)f(x)=ax2-lnx,
f′(x)=2ax-$\frac{1}{x}$,f(1)=a,f′(1)=2a-1,
故切线方程是:y-a=(2a-1)(x-1),
即y=(2a-1)x-a+1=x+b,
故2a-1=1,b=-a+1,
解得:a=1,b=0;
(2)f(x)的定义域是(0,+∞),
f′(x)=2ax-$\frac{1}{x}$,f′(2)=4a-$\frac{1}{2}$=0,解得:a=$\frac{1}{8}$,
∴f(x)=$\frac{1}{8}$x2-lnx,
f′(x)=$\frac{1}{4}$x-$\frac{1}{x}$=$\frac{(x+2)(x-2)}{4x}$,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,
故f(x)在[$\frac{1}{e}$,2]递减,在[2,e]递增,
故f(x)的最大值是f($\frac{1}{e}$)或f(e),
而f($\frac{1}{e}$)=$\frac{1}{{8e}^{2}}$-1<f(e)=$\frac{{e}^{2}}{8}$-1,
故函数的最大值是f(e)=$\frac{{e}^{2}}{8}$-1.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
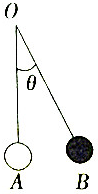 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )| A. | $\frac{1}{2}$,$\frac{1}{π}$ | B. | 2,$\frac{1}{π}$ | C. | $\frac{1}{2}$,π | D. | 2,π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极小值,无极大值 | B. | 有极大值,无极小值 | ||
| C. | 既有极小值,也有极大值 | D. | 既无极小值,也无极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com