
分析 椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1联立,利用椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1在第一象限内有两个不同的交点,确定a,b的关系,求出相应的面积,即可求出概率.
解答 解:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1联立,可得(b2+a2)x2-2a2x+a2-a2b2=0,
△=4a4-4(b2+a2)(a2-a2b2)>0,
∴b2+a2>1,
∵a,b在区间(0,1)内,
∴满足条件的区域的面积为1-$\frac{π}{4}$,
又a,b在区间(0,1)内,面积为1,
∴所求的概率为1-$\frac{π}{4}$.
故答案为:1-$\frac{π}{4}$.
点评 本题考查几何概型概率的计算,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
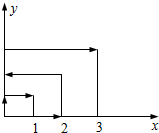 如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x2≥9,则x≥3或x≤-3 | B. | 若-3<x<3,则x2<9 | ||
| C. | 若x>3或x<-3,则x2>9 | D. | 若x≥3或x≤-3,则x2≥9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com