
分析 (1)利用函数有意义,建立不等式,求出m范围,即可求集合A;
(2)若A∩B=B,则B⊆A,分类讨论,即可求实数m的取值范围.
解答 解:(1)由题意,$\left\{\begin{array}{l}{x+2>0}\\{3-x>0}\end{array}\right.$,∴-2<x<3,∴A={x|-2<x<3};
(2)若A∩B=B,则B⊆A,
①B=∅,1-m$≥3m-1\$,∴m≤$\frac{1}{2}$;
②B≠∅,$\left\{\begin{array}{l}{1-m<3m-1}\\{1-m≥-2}\\{3m-1≤3}\end{array}\right.$,∴$\frac{1}{2}<m≤\frac{4}{3}$,
综上所述,m$≤\frac{4}{3}$.
点评 本题考查函数的定义域,考查集合的关系,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD中,平面PCD⊥平面ABCD,且PD=PC=$\frac{\sqrt{2}}{2}$CD=$\frac{\sqrt{2}}{2}$BC,∠BCD=$\frac{2π}{3}$,△ABD是等边三角形,AC∩BD=E.
已知四棱锥P-ABCD中,平面PCD⊥平面ABCD,且PD=PC=$\frac{\sqrt{2}}{2}$CD=$\frac{\sqrt{2}}{2}$BC,∠BCD=$\frac{2π}{3}$,△ABD是等边三角形,AC∩BD=E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{7}{3}π+3kπ,-\frac{1}{6}π+3kπ}],k∈Z$ | B. | $[{-\frac{5}{3}π+3kπ,-\frac{1}{6}π+3kπ}],k∈Z$ | ||
| C. | $[{-\frac{2}{3}π+2kπ,-\frac{1}{6}π+2kπ}],k∈Z$ | D. | $[{-\frac{1}{3}π+2kπ,-\frac{1}{6}π+2kπ}],k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
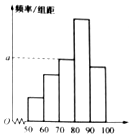 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com