
分析 (1)由奇函数的定义,f(x)+f(-x)=0,代入求得a的值,求得h(x)的解析式,求导,令h′(x)>0,即可求得h(x)单调增区间;
(2)由g(x)在区间[$\frac{π}{3}$,$\frac{2π}{3}$]是减函数,求导,g(′x)=λ+sinx(x∈[$\frac{π}{3}$,$\frac{2π}{3}$])上恒小于0,求得λ的取值范围,且函数g(x)的最大值是$\frac{π}{3}$λ-$\frac{1}{2}$≤λt-1,分离变量得t≤$\frac{π}{3}$+$\frac{1}{2λ}$,根据$\frac{π}{3}$+$\frac{1}{2λ}$在(-∞,-1)上是减函数,即可求得实数t的取值范围.
解答 解:(1)函数f(x)=ln(ex+a)(a为常数)是R上的奇函数.
f(x)+f(-x)=0,ln(ex+a)+ln(e-x+a)=0,即(ex+a)•(e-x+a)=1,
整理得:a(e-x+ex+a=)=0恒成立,解得:a=0,
f(x)=x,
h(x)=xe2f(x)=xe2x,
h′(x)=e2x(2x+1),
令h′(x)>0,解得:x>-$\frac{1}{2}$,
∴函数h(x)的单调递增区间为(-$\frac{1}{2}$,+∞);
(2)由(1)可知:a=0,g(x)=λx-cosx(x∈[$\frac{π}{3}$,$\frac{2π}{3}$])是减函数,
g(′x)=λ+sinx(x∈[$\frac{π}{3}$,$\frac{2π}{3}$])上恒小于0,
即λ<sinx,(x∈[$\frac{π}{3}$,$\frac{2π}{3}$])上恒成立,
解得:λ<-1,
g(x)=λx-cosx在区间[$\frac{π}{3}$,$\frac{2π}{3}$]上减函数,
故函数g(x)的最大值是$\frac{π}{3}$λ-$\frac{1}{2}$≤λt-1,
即t≤$\frac{π}{3}$+$\frac{1}{2λ}$,
由λ<-1,
$\frac{π}{3}$+$\frac{1}{2λ}$在(-∞,-1)上是减函数,
故t<$\frac{π}{3}$-$\frac{1}{2}$,
实数t的取值范围(-∞,$\frac{π}{3}$-$\frac{1}{2}$).
点评 本题卡从函数的单调性和奇偶性以及函数恒成立问题,考查导数在求函数的单调性及最值中的综合应用,考查转化思想,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -5或2 | B. | -1或4 | C. | -5或4 | D. | -5或-1或2或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
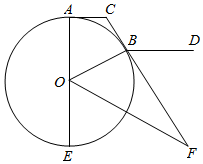 如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC.
如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
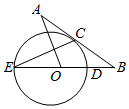 如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.
如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
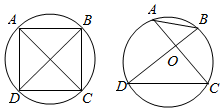 已知A,B,C,D是⊙O上的四个点
已知A,B,C,D是⊙O上的四个点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆O的直径,AC是圆O的切线,BC交圆O点E.
如图,AB是圆O的直径,AC是圆O的切线,BC交圆O点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com