
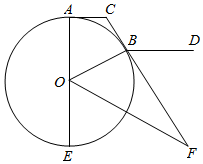
 如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC.
如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC.分析 (1)连接OC,运用切线的性质,可得△OAC≌△OBC,结合内角平分线的定义,可得∠FOC=90°,由直角三角形的射影定理,即可得证;
(2)由对角互补,可得四点C,A,O,B共圆,延长AC至M,运用两直线平行的性质,即可得证.
解答 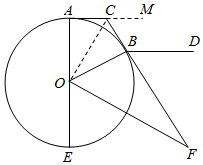 证明:(1)连接OC,由CA,CB为切线,可得CA=CB,
证明:(1)连接OC,由CA,CB为切线,可得CA=CB,
OA=OB,OC=OC,
即有△OAC≌△OBC,
即有∠AOC=∠BOC,
又OF平分∠BOE交CB的延长线于F,
可得∠EOF=∠BOF,
则∠FOC=∠FOB+∠BOC=∠EOF+∠AOC=90°,
在直角三角形COF中,OB为斜边CF上的高,
由射影定理,可得OB2=BC•BF;
(2)由∠CAO=∠CBO=90°,可得
四点C,A,O,B共圆,延长AC至M,
即有∠MCB=∠AOB,
由BD∥AC,可得∠DBF=∠MCB,
即有∠DBF=∠AOB.
点评 本题考查圆的切线的性质、四点共圆的判定和性质、直角三角形的射影定理的运用,考查推理和运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,4) | C. | $(-1,\frac{7}{2})$ | D. | (-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
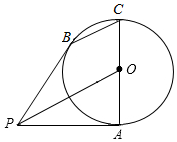 如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com