
分析 (1)求出f(x)的导数,求得切线的斜率,由两直线垂直的条件可得a=1,求导数,求单调区间和极值,令m<1<m+1,解不等式即可得到取值范围;
(2)问题转化为$\frac{1}{e+1}$$\frac{(x+1)(lnx+1)}{x}$>$\frac{{2e}^{x-1}}{{xe}^{x}+1}$,令h(x)=$\frac{(x+1)(lnx+1)}{x}$,m(x)=$\frac{{2e}^{x-1}}{{xe}^{x}+1}$,根据函数的单调性判断即可.
解答 解:(1)∵f′(x)=$\frac{1-a-lnx}{{x}^{2}}$,
f(x)在点(e,f(e))处的切线斜率为-$\frac{a}{{e}^{2}}$,
由切线与直线e2x-y+e=0垂直,
可得f′(e)=-$\frac{1}{{e}^{2}}$,即有-$\frac{a}{{e}^{2}}$=-$\frac{1}{{e}^{2}}$,
解得得a=1;
∴f(x)=$\frac{1+lnx}{x}$,f′(x)=-$\frac{lnx}{{x}^{2}}$(x>0)
当0<x<1,f′(x)>0,f(x)为增函数;
当x>1时,f′(x)<0,f(x)为减函数.
若f(x)在(m,m+1)上单调,
则m=0,或m>1.
(2)证明:g(x)=(x+1)•f(x)=(x+1)$\frac{a+lnx}{x}$,
当x>1时,g(x)>$\frac{2(e+1){e}^{x}}{e(x{e}^{x}+1)}$
即为 $\frac{1}{e+1}$$\frac{(x+1)(lnx+1)}{x}$>$\frac{{2e}^{x-1}}{{xe}^{x}+1}$,
令h(x)=$\frac{(x+1)(lnx+1)}{x}$,
则h′(x)=$\frac{x-lnx}{{x}^{2}}$,
再令φ(x)=x-lnx,则φ′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
∵x>1∴φ′(x)>0,φ(x)在(1,+∞)上是增函数,
∴φ(x)>φ(1)=1>0,h′(x)>0,
∴h(x)在(1,+∞)上是增函数,
∴x>1时,h(x)>h(1)=2
故 $\frac{h(x)}{e+1}$>$\frac{2}{e+1}$.
令m(x)=$\frac{{2e}^{x-1}}{{xe}^{x}+1}$,
则m′(x)=$\frac{{2e}^{x-1}(1{-e}^{x})}{{({xe}^{x}+1)}^{2}}$,
∵x>1,∴1-ex<0,m′(x)<0,即m(x)在(1,+∞)上是减函数,
∴x>1时,m(x)<m(1)=$\frac{2}{e+1}$,
∴g(x)>$\frac{2(e+1){e}^{x}}{e(x{e}^{x}+1)}$.
点评 本题考查导数的运用:求切线的斜率、单调区间和极值,同时考查构造函数求导数,判断单调性,运用单调性证明不等式,属于中档题.


科目:高中数学 来源: 题型:选择题
 已知函数y=f(x)在区间[a,b]的图象如图所示,则其导函数y=f′(x)在该区间( )
已知函数y=f(x)在区间[a,b]的图象如图所示,则其导函数y=f′(x)在该区间( )| A. | 先递减再递增 | B. | 先递增再递减 | ||
| C. | 先递增再递减最后又递增 | D. | 先递减再递增最后又递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
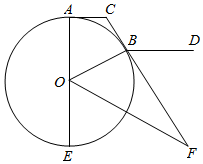 如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC.
如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
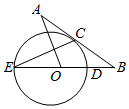 如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.
如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
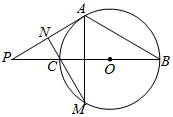 如图,直线PO与直径为4的圆O交于B,C两点,且PC=2,直线PA切圆O于点A
如图,直线PO与直径为4的圆O交于B,C两点,且PC=2,直线PA切圆O于点A查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.
如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com