
 如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.
如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.分析 (Ⅰ)由切割线定理,得MA2=MB•MC,再根据M为PA的中点,将MA换成MP,得到△PMB∽△CMP,从而∠MPB=∠MCP,最后在△CMP中利用内角和为180°列式,可得∠MPB的大小;
(Ⅱ)证明△MAB~△MCA,可得$\frac{{{S_{△MAB}}}}{{{S_{△MCA}}}}=\frac{{M{A^2}}}{{M{C^2}}}$,即可求$\frac{{{S_{△MAB}}}}{{{S_{△MCA}}}}$.
解答 解:(Ⅰ)∵MA是圆O的切线,MC是圆O的割线,∴MA2=MB•MC,
又∵M为AP的中点,∴MA=MP,
∴MP2=MB•MC,且∠PMB=∠CMP,
∴△PMB~△CMP,∴∠MPB=∠MCP,
又∵∠MPB+∠MCP+∠CMP+∠CPB=180°,
且∠BMP=120°,∠BPC=30°,∴∠MPB=15°.
(Ⅱ)∵MA是圆O的切线,∴∠MAB=∠ACM,
∴△MAB~△MCA,
∴$\frac{{{S_{△MAB}}}}{{{S_{△MCA}}}}=\frac{{M{A^2}}}{{M{C^2}}}$,
在△CMP中,MC=8,∠CPM=45°,∠PCM=15°,
由正弦定理得:$MP=4(\sqrt{3}-1)$,∵MA=MP,∴$MA=4(\sqrt{3}-1)$,
∴$\frac{{{S_{△MAB}}}}{{{S_{△MCA}}}}=\frac{{M{A^2}}}{{M{C^2}}}=\frac{{{{[4(\sqrt{3}-1)]}^2}}}{8^2}=\frac{{2-\sqrt{3}}}{2}$.
点评 本题给出圆的切线和割线,在已知两个角的度数情况下求未知角的度数,求$\frac{{{S_{△MAB}}}}{{{S_{△MCA}}}}$.着重考查了三角形的相似、切割线定理和三角形内角和定理等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
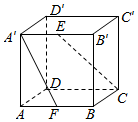 如图,在棱长为2的正方体ABCD-A′B′C′D′中,E、F分别是A′B′和AB的中点.求:
如图,在棱长为2的正方体ABCD-A′B′C′D′中,E、F分别是A′B′和AB的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F.
如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
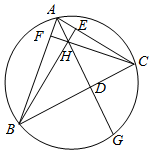 如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G.
如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com