
分析 (1)根据函数y=f(x)的最大值得出A的值,根据函数y=f(x)的图象与x轴的任意两个相邻交点间的距离求出周期T与ω的值,
再求出φ的值,即得f(x)的解析式与单调增区间;
(2)求出$x∈[{-\frac{π}{3},\frac{π}{2}}]$时x+$\frac{π}{6}$的范围,再求出sin(x+$\frac{π}{6}$)的取值范围,即得函数f(x)的值域.
解答 解:(1)因为当$x=\frac{π}{3}$时,函数y=f(x)取得最大值2,所以A=2,…2分
因为函数y=f(x)的图象与x轴的任意两个相邻交点间的距离为π,
所以T=2π,即$\frac{2π}{ω}=2π$,所以ω=1,…4分
将点$(\frac{π}{3},2)$代入f(x)=2sin(x+φ),得$sin(\frac{π}{3}+φ)=1$,
因为0<φ<π,所以$φ=\frac{π}{6}$,
所以$f(x)=2sin(x+\frac{π}{6})$;…6分
令-$\frac{π}{2}$+2kπ≤x≤$\frac{π}{2}$+2kπ,k∈Z,
解得-$\frac{2π}{3}$+2kπ≤x≤$\frac{π}{3}$+2kπ,k∈Z;
所以f(x)的单调增区间是$[{2kπ-\frac{2π}{3},2kπ+\frac{π}{3}}],(k∈z)$; …10分
(2)当$x∈[{-\frac{π}{3},\frac{π}{2}}]$时,$x+\frac{π}{6}∈[{-\frac{π}{6},\frac{2π}{3}}]$,
$sin(x+\frac{π}{6})∈[{-\frac{1}{2},1}]$,…14分
所以函数f(x)的值域是[-1,2]. …16分
点评 本题考查了三角函数y=Asin(ωx+φ)的图象与性质的应用问题,是基础题目.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
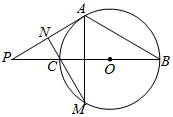 如图,直线PO与直径为4的圆O交于B,C两点,且PC=2,直线PA切圆O于点A
如图,直线PO与直径为4的圆O交于B,C两点,且PC=2,直线PA切圆O于点A查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.
如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA是⊙O的切线,切点为A,PB,PC是⊙O的割线,它们与⊙O分别交于B,D和C,E,延长CD交PA于M,∠MPC=∠MDP.
如图,PA是⊙O的切线,切点为A,PB,PC是⊙O的割线,它们与⊙O分别交于B,D和C,E,延长CD交PA于M,∠MPC=∠MDP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
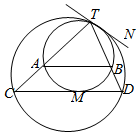 如图所示,两个圆相内切于点T,公切线为TN,过内圆上一点M,做内圆的切线,交外圆于C,D两点,TC,TD分别交内圆于A,B两点.
如图所示,两个圆相内切于点T,公切线为TN,过内圆上一点M,做内圆的切线,交外圆于C,D两点,TC,TD分别交内圆于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 偏好理 | 偏好文 | 总计 | |
| 男 | 20 | 25 | |
| 女 | 13 | ||
| 总计 | 50 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com