
| 偏好理 | 偏好文 | 总计 | |
| 男 | 20 | 25 | |
| 女 | 13 | ||
| 总计 | 50 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)有表中数据,由男生总计有25人,偏好理的20,则偏好文的有5人,总计有50人,男生25人,女生有25,偏好文的15,则偏好理的12人,即可将列联表补充补充完整;
(Ⅱ)利用公式求得K2,与临界值比较,即可得到结论.
解答 解:(Ⅰ)由男生总计有25人,偏好理的20,则偏好文的有5人,
总计有50人,男生25人,女生有25,偏好文的15,则偏好理的12人,
则列联表补充如下:
| 偏好理 | 偏好文 | 总计 | |
| 男 | 20 | 5 | 25 |
| 女 | 12 | 13 | 25 |
| 总计 | 32 | 18 | 50 |
点评 本题考查独立性检验知识,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
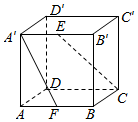 如图,在棱长为2的正方体ABCD-A′B′C′D′中,E、F分别是A′B′和AB的中点.求:
如图,在棱长为2的正方体ABCD-A′B′C′D′中,E、F分别是A′B′和AB的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 男 | 5 | ||
| 女 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 回答 正确 的人数 | 回答正确 的人数占本 组的频率 | 频率正确直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 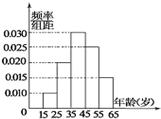 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65) | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com