
 如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,分析 (Ⅰ)利用圆的切线的判定方法,证明OC⊥FC,即可证明:FC是⊙O的切线;
(Ⅱ)若FB=FE,⊙O的半径为$\sqrt{2}$,利用切割线定理、勾股定理求FC.
解答 证明:(Ⅰ)连接OC.
∵AB是直径,
∴∠ACB=90°,
又∵F是BD中点,
∴∠BCF=∠CBF,
又OC=OB
∴∠OBC=∠OCB,
从而∠FCB+∠BCO=∠FBC+∠CBO=90°,
即:OC⊥FC,FC是⊙O的切线.
解:(Ⅱ)延长直线CF交直线AB于点G,
由FC=FB=FE得:∠FCE=∠FEC,
又∠FCE=∠GFB,∠FEC=∠AFB,
∴∠GFB=∠AFB
从而△AGF是等腰三角形,$GB=AB=2\sqrt{2}$.
由切割线定理得:${(FC+FG)^2}=GB•GA=2\sqrt{2}×4\sqrt{2}=16$.…①
在Rt△BGF中,由勾股定理得:FG2=FC2+8…②
由①、②得:FC=1.
点评 本题考查圆的切线的判定,切割线定理,平行线的性质定理,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
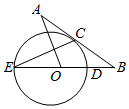 如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.
如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.
如图,自圆O外一点P引圆O的切线,切点为A,M为AP的中点,过点M引圆的割线交圆O于B,C两点,且∠BMP=120°,∠BPC=30°,MC=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆O的直径,AC是圆O的切线,BC交圆O点E.
如图,AB是圆O的直径,AC是圆O的切线,BC交圆O点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA是⊙O的切线,切点为A,PB,PC是⊙O的割线,它们与⊙O分别交于B,D和C,E,延长CD交PA于M,∠MPC=∠MDP.
如图,PA是⊙O的切线,切点为A,PB,PC是⊙O的割线,它们与⊙O分别交于B,D和C,E,延长CD交PA于M,∠MPC=∠MDP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
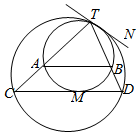 如图所示,两个圆相内切于点T,公切线为TN,过内圆上一点M,做内圆的切线,交外圆于C,D两点,TC,TD分别交内圆于A,B两点.
如图所示,两个圆相内切于点T,公切线为TN,过内圆上一点M,做内圆的切线,交外圆于C,D两点,TC,TD分别交内圆于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 偏好理 | 偏好文 | 总计 | |
| 男 | 20 | 25 | |
| 女 | 13 | ||
| 总计 | 50 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com