
���� ��I��������M�IJ�������Ϊ$\left\{\begin{array}{l}x=cos��\\ y=sin��\end{array}$������Ϊ������������[0����]������cos2��+sin2��=1�ɵ���ͨ���̣�ע��y��ȡֵ��Χ������N�ļ����귽��Ϊ��sin����+$\frac{��}{4}$��=$\frac{\sqrt{2}}{2}$m������mΪ��������չ���ɵã�$\frac{\sqrt{2}}{2}����sin��+��cos�ȣ�$=$\frac{\sqrt{2}}{2}$m����x=��cos�ȣ�y=��sin�ȴ���ɵ�ֱ�����귽�̣�
����I����ֱ��N��ԲM����ʱ��$\frac{|m|}{\sqrt{2}}$=1��ȡm=$\sqrt{2}$��ֱ�߾����㣨1��0��ʱ��m=1�����ɵó�m��ȡֵ��Χ��
��� 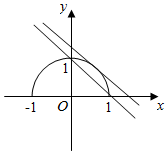 �⣺��I��������M�IJ�������Ϊ$\left\{\begin{array}{l}x=cos��\\ y=sin��\end{array}$������Ϊ������������[0����]���ɵ�x2+y2=1��1��y��0��
�⣺��I��������M�IJ�������Ϊ$\left\{\begin{array}{l}x=cos��\\ y=sin��\end{array}$������Ϊ������������[0����]���ɵ�x2+y2=1��1��y��0��
����N�ļ����귽��Ϊ��sin����+$\frac{��}{4}$��=$\frac{\sqrt{2}}{2}$m������mΪ��������չ���ɵã�$\frac{\sqrt{2}}{2}����sin��+��cos�ȣ�$=$\frac{\sqrt{2}}{2}$m����Ϊ��x+y=m��
����I����ֱ��N��ԲM����ʱ��$\frac{|m|}{\sqrt{2}}$=1��ȡm=$\sqrt{2}$��
ֱ�߾����㣨1��0��ʱ��m=1��
������M������N�����������㣬��m��ȡֵ��Χ��[1��$\sqrt{2}$����
���� ���⿼����ֱ�������뼫����Ļ������������̻�Ϊ��ͨ���̡�ֱ����Բ�ཻ�������⣬������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
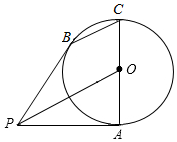 ��ͼ����֪�߶�ACΪ��O��ֱ����PAΪ��O�����ߣ��е�ΪA��BΪ��O��һ�㣬��BC��PO��
��ͼ����֪�߶�ACΪ��O��ֱ����PAΪ��O�����ߣ��е�ΪA��BΪ��O��һ�㣬��BC��PO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
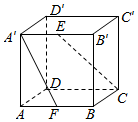 ��ͼ�����ⳤΪ2��������ABCD-A��B��C��D���У�E��F�ֱ���A��B���AB���е㣮��
��ͼ�����ⳤΪ2��������ABCD-A��B��C��D���У�E��F�ֱ���A��B���AB���е㣮���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
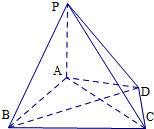 ��֪����P-ABCD��ͼ��ʾ������ƽ��PAD��ƽ��ABCD��PA��AD��PA=AB=BC=AC=4���߶�AC���߶�BDƽ�֣�
��֪����P-ABCD��ͼ��ʾ������ƽ��PAD��ƽ��ABCD��PA��AD��PA=AB=BC=AC=4���߶�AC���߶�BDƽ�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Բ�ڽ��ı���ABCD�У�BD��Բ��ֱ����AB=AC���ӳ�AD��BC���ӳ����ཻ�ڵ�E����EF��BD��F��
��ͼ��Բ�ڽ��ı���ABCD�У�BD��Բ��ֱ����AB=AC���ӳ�AD��BC���ӳ����ཻ�ڵ�E����EF��BD��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��C����ABΪֱ���İ�ԲO��һ�㣬CH��AB�ڵ�H��ֱ��AC���B��������ཻ�ڵ�D��FΪBD�е㣬����AF��CH�ڵ�E��
��ͼ����֪��C����ABΪֱ���İ�ԲO��һ�㣬CH��AB�ڵ�H��ֱ��AC���B��������ཻ�ڵ�D��FΪBD�е㣬����AF��CH�ڵ�E���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com