
| ���ķμ��� | �����ķμ��� | �ϼ� | |
| �� | 5 | ||
| Ů | 10 | ||
| �ϼ� | 50 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1���������֪����ȫ��50���������ȡ1�ˣ��鵽���ķμ������˵ĸ���Ϊ$\frac{3}{5}$��������û��ķμ�����Ϊ30�ˣ��������2��2��������
��2���ٴ��빫ʽ����ó�K2����7.879�Ƚϼ��ɵó����ۣ�
��3���ڻ��ķμ�����10λŮ���У���3λ�ֻ���θ������ѡ����θ����Ů������Ϊx����η��ӳ����ηֲ������ɵõ�x�ķֲ��к���ѧ������
��� �⣺��1��������ȫ��50���������ȡ1�ˣ��鵽���ķμ������˵ĸ���Ϊ$\frac{3}{5}$���ɵû��ķμ�����Ϊ30�ˣ��ʿɵ��������������£�
| ���ķμ��� | �����ķμ��� | �ϼ� | |
| �� | 20 | 5 | 25 |
| Ů | 10 | 15 | 25 |
| �ϼ� | 30 | 20 | 50 |
| x | 0 | 1 | 3 | |
| P | $\frac{7}{24}$ | $\frac{21}{40}$ | $\frac{7}{40}$ | $\frac{1}{120}$ |
���� ���⿼������Լ����Ӧ�����⣬������������÷ֲ��к���ѧ����������ѧ���ļ�������������ѧ�������������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB��ԲO��ֱ����AC��ԲO�����ߣ�BC��ԲO��E��
��ͼ��AB��ԲO��ֱ����AC��ԲO�����ߣ�BC��ԲO��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
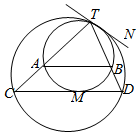 ��ͼ��ʾ������Բ�������ڵ�T��������ΪTN������Բ��һ��M������Բ�����ߣ�����Բ��C��D���㣬TC��TD�ֱ���Բ��A��B���㣮
��ͼ��ʾ������Բ�������ڵ�T��������ΪTN������Բ��һ��M������Բ�����ߣ�����Բ��C��D���㣬TC��TD�ֱ���Բ��A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ƫ���� | ƫ���� | �ܼ� | |
| �� | 20 | 25 | |
| Ů | 13 | ||
| �ܼ� | 50 |
| P��K2��k0�� | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�5] | B�� | ��-�ޣ�4] | C�� | ��-�ޣ�2] | D�� | ��-�ޣ�1] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com