
分析 (1)由曲线C1:$\left\{\begin{array}{l}{x=a(cosφ+sinφ)}\\{y=a(sinφ-cosφ)}\end{array}\right.$,(φ为参数,a>0),平方相加可得可得x2+y2=a2=a2.曲线C2:ρsin(θ+$\frac{π}{6}$)=1,展开可得:$\frac{\sqrt{3}}{2}ρsinθ+\frac{1}{2}ρcosθ$=1,把y=ρsinθ,x=ρcosθ代入即可化为直角坐标方程.
(2)圆心(0,0)到直线的距离d=$\frac{2}{2}$=1.根据曲线C1上恰好存在四个不同的点到曲线C2的距离相等,可得直线两侧各有两个点到直线的距离为1,因此$\sqrt{2}a$-1>1,解出即可得出.
解答 解:(1)由曲线C1:$\left\{\begin{array}{l}{x=a(cosφ+sinφ)}\\{y=a(sinφ-cosφ)}\end{array}\right.$,(φ为参数,a>0),
可得x2+y2=a2(1+sin2φ)+a2(1-sin2φ)=a2.
曲线C2:ρsin(θ+$\frac{π}{6}$)=1,展开可得:$\frac{\sqrt{3}}{2}ρsinθ+\frac{1}{2}ρcosθ$=1,
化为直角坐标方程:$\sqrt{3}$y+x=2.
(2)圆心(0,0)到直线的距离d=$\frac{2}{2}$=1.
∵曲线C1上恰好存在四个不同的点到曲线C2的距离相等,
∴直线两侧各有两个点到直线的距离为1,
∴$\sqrt{2}a$-1>1,解得$a>\sqrt{2}$.
故a的取值范围是$(\sqrt{2},+∞)$.
点评 本题考查了极坐标化为直角坐标方程、圆的参数方程化为普通方程、点到直线的距离公式、三角函数化简求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 男 | 5 | ||
| 女 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
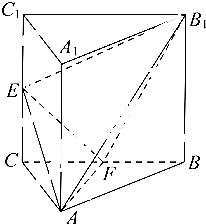 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1=2,E,F分别是CC1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
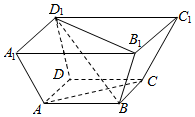 上海世博会中国馆的标志性建筑物的上层框图如图所示,其上下底面是平行的两正方形,上下底面的中心连线垂直于上下底面,且各侧棱均相等,(即为正棱台),经侧量得知2AB=A1B1=12,侧棱长为$\sqrt{34}$.
上海世博会中国馆的标志性建筑物的上层框图如图所示,其上下底面是平行的两正方形,上下底面的中心连线垂直于上下底面,且各侧棱均相等,(即为正棱台),经侧量得知2AB=A1B1=12,侧棱长为$\sqrt{34}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com