
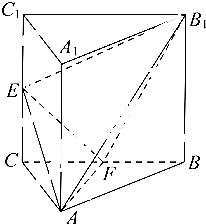
 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1=2,E,F分别是CC1,BC的中点.分析 (1)推导出AF⊥EF,B1F⊥EF,由此能证明EF⊥平面AB1F.
(2)过点F作FP⊥AE,连结B1P,则∠B1PF就是二面角B1-AE-F的平面角,由此能求出锐二面角B1-AE-F的余弦值.
(3)∴将侧面BB1A沿BA展开为BAO,使得BAO与平面BAC共面时,|FM|+|MB1|的最小值为OF,由此能求出结果.
解答 证明:(1)∵三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,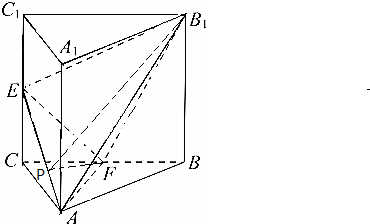
∠BAC=90°且AB=AA1=2,E,F分别是CC1,BC的中点,
∴由条件知AF⊥平面CC1BB1,∴AF⊥EF,
由勾股定理得B1F=$\sqrt{6}$,EF=$\sqrt{3}$,B1E=3,
∵${B}_{1}{E}^{2}={{B}_{1}F}^{2}+E{F}^{2}$,∴B1F⊥EF,
又∵B1F∩AF=F,
∴EF⊥平面AB1F.
解:(2)过点F作FP⊥AE,连结B1P,
∵EA⊥PF,EA⊥B1F,∴EA⊥平面B1PF,∴EA⊥B1P,
∴∠B1PF就是二面角B1-AE-F的平面角,
由题意得PF=$\frac{\sqrt{30}}{5}$,B1P=$\frac{6\sqrt{5}}{5}$,
∴cos∠B1PF=$\frac{PF}{{B}_{1}P}$=$\frac{\sqrt{6}}{6}$,
∴锐二面角B1-AE-F的余弦值为$\frac{\sqrt{6}}{6}$.
(3)∵点M是AB上一点,
∴将侧面BB1A沿BA展开为BAO,
使得BAO与平面BAC共面时,|FM|+|MB1|的最小值为OF,
在△BFO中,BF=$\sqrt{2}$,BO=2,∠FBO=135°,
∴OF=$\sqrt{2+4-2×2×\sqrt{2}×cos135°}$=$\sqrt{10}$.
∴|FM|+|MB1|的最小值为$\sqrt{10}$.
点评 本题考查的知识点是直线与平面垂直的判定及二面角的平面角的求法,其中在求二面角时,找出二面角的平面角是解答本题的关键


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
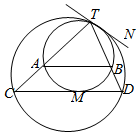 如图所示,两个圆相内切于点T,公切线为TN,过内圆上一点M,做内圆的切线,交外圆于C,D两点,TC,TD分别交内圆于A,B两点.
如图所示,两个圆相内切于点T,公切线为TN,过内圆上一点M,做内圆的切线,交外圆于C,D两点,TC,TD分别交内圆于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5] | B. | (-∞,4] | C. | (-∞,2] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B,C两点,弦CD∥AP,AD,BC相交于点E,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B,C两点,弦CD∥AP,AD,BC相交于点E,F为CE上一点,且DE2=EF•EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com