解法一:假设(1-a)b,(1-b)c,(1-c)a都大于
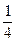
,
则(1-a)b·(1-b)c·(1-c)a>
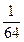
∵0<a<1,
∴a>0,1-a>0。
∴0<a(1-a)≤[
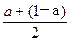
]
2=
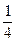
同理0<b(1-b)≤
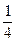
,0<c(1-c)≤
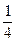
,
三式相乘得:0<(1-a)b·(1-b)c·(1-c)a≤
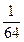
②
①与②矛盾,故假设不成立
∴(1-a)b,(1-b)c,(1-c)a中至少有一个不大于
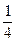
解法二:假设:假设(1-a)b,(1-b)c,(1-c)a都大于
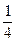
,
∵0<a<1,0<b<1,
∴(1-a)+b≥
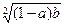
>
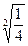
=1
同理(1-b)+c>1,(1-c)+a>1
三式相加得:(1-a)+b+(1-b)+c+(1-c)+a>3
即3>3,不等式不成立,故假设不成立。

 。
。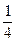 ,
,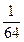
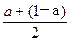 ]2=
]2=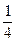
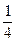 ,0<c(1-c)≤
,0<c(1-c)≤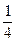 ,
,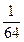 ②
②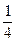
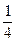 ,
,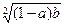 >
>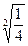 =1
=1
