
分析 先根据基本不等式可得 $\frac{a+b}{2}$≥$\sqrt{ab}$>0,$\frac{b+c}{2}$≥$\sqrt{bc}$>0,$\frac{a+c}{2}$≥$\sqrt{ac}$>0,然后根据不等式的性质可得 $\frac{a+b}{2}$•$\frac{b+c}{2}$•$\frac{a+c}{2}$>abc成立,两边同取常用对数,即可证得结论.
解答 证明:∵a,b,c∈R+,
∴$\frac{a+b}{2}$≥$\sqrt{ab}$>0,$\frac{b+c}{2}$≥$\sqrt{bc}$>0,$\frac{a+c}{2}$≥$\sqrt{ac}$>0…(4分)
又上述三个等式中等号不能同时成立
∴$\frac{a+b}{2}$•$\frac{b+c}{2}$•$\frac{a+c}{2}$>abc成立.…(6分)
ln( $\frac{a+b}{2}$•$\frac{b+c}{2}$•$\frac{a+c}{2}$)>ln(abc)
∴ln$\frac{a+b}{2}$+ln$\frac{b+c}{2}$+ln$\frac{c+a}{2}$>lna+lnb+lnc.…(12分)
点评 本题主要考查了对数函数性质的综合应用,以及基本不等式的应用,同时考查了转化的数学思想,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{2}{3}$π | C. | $\frac{5}{6}$π | D. | $\frac{3}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
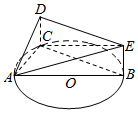 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36πcm2 | B. | 27πcm2 | C. | 20πcm2 | D. | 12πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com