
分析 (1)如图所示,当α=$\frac{π}{3}$时,经过1次操作到A1点,经过2次操作到A2点,利用多边形外角和定理及其向量多边形法则即可得出.
(2)根据多边形外角和定理α=$\frac{2π}{10}$.
解答 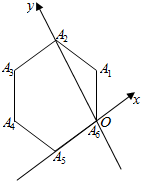 解:(1)如图所示,
解:(1)如图所示,
当α=$\frac{π}{3}$时,经过1次操作到A1点,经过2次操作到A2点,
6α=2π(多边形外角和定理).
∴$\overrightarrow{O{A}_{1}}$+$\overrightarrow{{A}_{1}{A}_{2}}$+…+$\overrightarrow{{A}_{5}{A}_{6}}$=$\overrightarrow{0}$,
因此当α=$\frac{π}{3}$时,经过6次操作才能回到原点.
(2)根据多边形外角和定理α=$\frac{2π}{10}$=$\frac{π}{5}$.
∴存在α=$\frac{π}{5}$,使机器人经过10次操作,能首次回到原点.
点评 本题考查了多边形外角和定理、向量的多边形法则,考查了数形结合方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {α|α=k•360°+456°,k∈Z} | B. | {α|α=k•360°+264°,k∈Z} | ||
| C. | {α|α=k•360°+96°,k∈Z} | D. | {α|α=k•360°-264°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=$\frac{1}{x}$ | C. | y=-x3 | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{1}{e}-1})$ | B. | $({-∞,-\frac{1}{e}})$ | C. | $({-∞,-\frac{1}{e}-2})$ | D. | $({-∞,-\frac{1}{e}-2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x+4≥0 | B. | $?{x_0}∈R,x_0^2-2{x_0}+4>0$ | ||
| C. | ?x∉R,x2-2x+4≤0 | D. | $?{x_0}∉R,x_0^2-2{x_0}+4>0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com