已知命题p:?x∈R.x2-2x+4≤0.则?p为( )A．?x∈R.x2-2x+4≥0B．$?{x 0}∈R.x 0^2-2{x 0}+4＞0$C．?x∉R.x2-2x+4≤0D．$?{x 0}∉R.x 0^2-2{x 0}+4＞0$ 题目和参考答案——青夏教育精英家教网—

18．已知命题p：?x∈R，x²-2x+4≤0，则?p为（　　）

	A．	?x∈R，x²-2x+4≥0		B．	$?{x_0}∈R，x_0^2-2{x_0}+4＞0$
	C．	?x∉R，x²-2x+4≤0		D．	$?{x_0}∉R，x_0^2-2{x_0}+4＞0$

分析利用全称命题的否定是特称命题写出结果即可．

解答解：因为全称命题的否定是特称命题，所以，命题p：?x∈R，x²-2x+4≤0，则?p为：$?{x_0}∈R，x_0^2-2{x_0}+4＞0$．
故选：B．

点评本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

8．2012年全国中学生机器人大赛选选拔赛中，机器人刚开始在原点位置，为了让机器人完成某项任务，学生给机器人设置了以下指令：先逆时针旋转α角，然后向前进1米，将该指令进行一次称为一次操作，试用向量解决以下问题．
（1）当α=$\frac{π}{3}$时，经过几次操作才能回到原点？
（2）是否存在α，使机器人经过10次操作，能首次回到原点？

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．位于平面直角坐标系原点的一个质点P按下列规则移动：质点每次移动一个单位，移动的方向是向上或向下，并且向上移动的概率为$\frac{1}{4}$，则质点P移动4次后位于点（0，2）的概率是（　　）

A．

$\frac{1}{256}$

B．

$\frac{3}{256}$

C．

$\frac{9}{256}$

D．

$\frac{3}{64}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．在△ABC中，已知∠A=45°，cosB=$\frac{\sqrt{10}}{10}$．
（1）求cosC；
（2）若BC=5，求AC的长．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．已知向量$\overrightarrow{OP}$=（2cosx+1，cos2x-sinx+1），$\overrightarrow{OQ}$=（cosx，-1），定义f（x）=$\overrightarrow{OP}$•$\overrightarrow{OQ}$．
（1）求f（x）的最小正周期；
（2）求f（x）的最大值和最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知关于x的函数f（x）=（a+1）x²-ax+a-1，a∈R是常数．
（1）当a=1时，求不等式f（x）＞0的解集；
（2）若?x∈R，都有f（x）＜2x²，求a的取值范围（用集合表示）．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．把300毫升溶液分给5个实验小组，使每组所得成等差数列，且较多三组之和的$\frac{1}{7}$是较少两组之和，则最少的那个组分得溶液5毫升．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．已知定义在R上的函数f（x）满足：f（x+y）=f（x）+f（y），当x＜0时，f（x）＜0．求证：f（x）是奇函数．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

8．

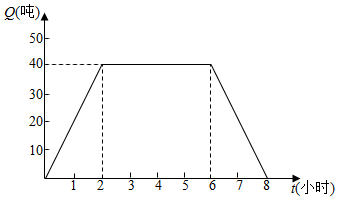某游泳池先开进水管注水，使用完毕后开排水管排水，存水量Q（吨）与时间t（小时）之间的函数关系如图，则Q关于t的函数解析式为Q（t）=$\left\{\begin{array}{l}{20t，}&{0≤t≤2}\\{40，}&{2＜t＜5}\\{-\frac{40}{3}t+\frac{320}{3}，}&{5＜t≤8}\end{array}\right.$．

查看答案和解析>>

同步练习册答案