练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有（ ）

    ①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人；

    ②用简单随机抽样的方法从新生中选出100人；

    ③西部地区学生小刘被选中的概率为；

    ④中部地区学生小张被选中的概率为

    A. ①④ B. ①③ C. ②④ D. ②③

    【答案】B

    【解析】分析：由题意逐一考查所给的说法是否正确即可.

    详解：逐一考查所给的说法：

    ①由分层抽样的概念可知，取东部地区学生48人、

    中部地区学生32人、

    西部地区学生20人，题中的说法正确；

    ②新生的人数较多，不适合用简单随机抽样的方法抽取人数，题中的说法错误；

    ③西部地区学生小刘被选中的概率为，题中的说法正确；

    ④中部地区学生小张被选中的概率为，题中的说法错误；

    综上可得，正确的说法是①③.

    本题选择B选项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，（是的导函数），在上的最大值为.

    （1）求实数的值；

    （2）判断函数在内的极值点个数，并加以证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知焦点在x轴上的椭圆C1的长轴长为8,短半轴为2,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点．

    (1)求抛物线C2的标准方程；

    (2)过（1，0）的两条相互垂直的直线与抛物线C2有四个交点,求这四个点围成四边形的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】人站成两排队列，前排人，后排人.

    （1）一共有多少种站法；

    （2）现将甲、乙、丙三人加入队列，前排加一人，后排加两人，其他人保持相对位置不变，求有多少种不同的加入方法.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象经过点，且在点处的切线方程为.

    （1）求函数的解析式；

    （2）求函数的单调区间

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究.该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).

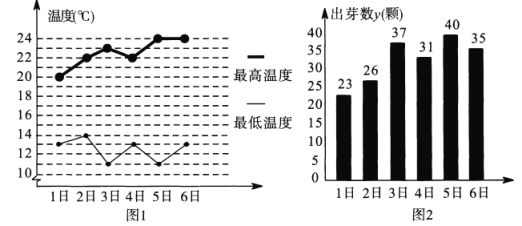
    根据上述数据作出散点图,可知绿豆种子出芽数 (颗)和温差 ()具有线性相关关系.

    (1)求绿豆种子出芽数 (颗)关于温差 ()的回归方程；

    (2)假如4月1日至7日的日温差的平均值为11,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.

    附：，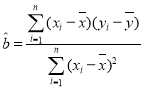

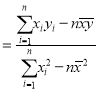    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知．

    （1）求f（f（1）），f（f（1））；

    （2）画出f（x）的图象；

    （3）若f（x）=a，问a为何值时，方程没有根？有一个根？两个根？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线：与直线：的距离为，椭圆：的离心率为.

    （1）求椭圆的标准方程；

    （2）在（1）的条件下，抛物线：的焦点与点关于轴上某点对称，且抛物线与椭圆在第四象限交于点，过点作抛物线的切线，求该切线方程并求该直线与两坐标轴围成的三角形面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的公差不为0，其前项和为，，且，，成等比数列.

    （1）求数列的通项公式及的最小值；

    （2）若数列是等差数列，且，求的值.

    查看答案和解析>>

    同步练习册答案