
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)首先由a,b的值确定所有基本事件,由![]() 可得到满足条件的点,求其比值可得到概率值;(Ⅱ)由等腰三角形分情况讨论可得到构成三角形的个数,从而求得相应的概率
可得到满足条件的点,求其比值可得到概率值;(Ⅱ)由等腰三角形分情况讨论可得到构成三角形的个数,从而求得相应的概率
试题解析:先后2次抛掷一枚骰子,将得到的点数分别记为![]() 包含的基本事件有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),…,(6,5),(6,6),共36个.………………………2分
包含的基本事件有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),…,(6,5),(6,6),共36个.………………………2分
(Ⅰ)由于![]() ,
,
∴满足条件的情况只有![]() ,或
,或![]() 两种情况. ……………4分
两种情况. ……………4分
∴满足![]() 的概率为
的概率为![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)∵三角形的一边长为5,三条线段围成等腰三角形,
∴当![]() 时,
时, ![]() ,共1个基本事件;
,共1个基本事件;
当![]() 时,
时, ![]() ,共1个基本事件;
,共1个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
当![]() 时,
时, ![]() ,共6个基本事件;
,共6个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
∴满足条件的基本事件共有1+1+2+2+6+2=14个.…………………………11分
∴三条线段能围成等腰三角形的概率为![]() .…………………………………12分
.…………………………………12分


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】对绵阳南山实验学校的500名教师的年龄进行统计分析,年龄的频率分布直方图如图所示,规定年龄在![]() 内的为青年教师,
内的为青年教师,![]() 内的为中年教师,
内的为中年教师,![]() 内的为老年教师.
内的为老年教师.
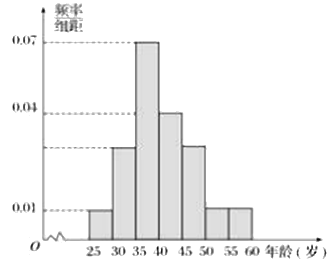
(1)求年龄![]() ,
,![]() 内的教师人数;
内的教师人数;
(2)现用分层抽样的方法从中、青年中抽取18人进行同课异构课堂展示,求抽到年龄在![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名学生每天骑车上学,从他家里到学校的途中有6个交通岗,假设在每个交通岗遇到红灯的事件是相互独立的,并且概率都是![]() .
.
(1)假设![]() 为这名学生在途中遇到红灯的次数,求
为这名学生在途中遇到红灯的次数,求![]() 的分布列;
的分布列;
(2)设![]() 为这名学生在首次停车前经过的路口数,求
为这名学生在首次停车前经过的路口数,求![]() 的分布列;
的分布列;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了300名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 180 | ||
女大学生 | 45 | ||
合计 | 200 |
(Ⅰ)根据题意完成表格;
(Ⅱ)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
附:![]() ,
,![]()
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | .072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的两个焦点为
)的两个焦点为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
, ![]() 在椭圆上,
在椭圆上, ![]() 在线段
在线段![]() 上,且
上,且![]() 的周长等于
的周长等于![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过圆![]() :
: ![]() 上任意一点
上任意一点![]() 作椭圆
作椭圆![]() 的两条切线
的两条切线![]() 和
和![]() 与圆
与圆![]() 交于点
交于点![]() ,
, ![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com