
分析 (1)当a=-2时,f(x)<g(x)等价于$\left\{\begin{array}{l}{x<1}\\{3-2x<\frac{1}{2}x+3}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x≤2}\\{1<\frac{1}{2}x+3}\end{array}\right.$或$\left\{\begin{array}{l}{x>2}\\{2x-3<\frac{1}{2}x+3}\end{array}\right.$,由此能求出不等式f(x)<g(x)的解集.
(2)推导出f(x)=a+1,不等式f(x)≤a+1≤($\frac{1}{2}x+3$)max,由此能求出实数a的取值范围.
解答 解:(1)当a=-2时,
f(x)=|x-1|+|x-2|=$\left\{\begin{array}{l}{3-2x,x<1}\\{1,1≤x≤2}\\{2x-3,x>2}\end{array}\right.$,
∴f(x)<g(x)等价于$\left\{\begin{array}{l}{x<1}\\{3-2x<\frac{1}{2}x+3}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x≤2}\\{1<\frac{1}{2}x+3}\end{array}\right.$或$\left\{\begin{array}{l}{x>2}\\{2x-3<\frac{1}{2}x+3}\end{array}\right.$,
解得0<x<1或1≤x≤2或2<x<4,即0<x<4.
∴不等式f(x)<g(x)的解集为{x|0<x<4}.
(2)∵x∈[-a,1],∴f(x)=1-x+x+a=a+1,
不等式f(x)=a+1≤g(x)max=($\frac{1}{2}x+3$)max,
∴-1<a≤$\frac{5}{2}$,
∴实数a的取值范围是(-1,$\frac{5}{2}$].
点评 本题考查零点分段法求解绝对值不等式,考查分类讨论,是中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于点($\frac{5π}{12}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
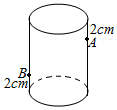 圆柱形玻璃杯高8cm,杯口周长为12cm,内壁距杯口2cm的点A处有一点蜜糖.A点正对面的外壁(不是A点的外壁)距杯底2cm的点B处有一小虫.若小虫沿杯壁爬向蜜糖饱食一顿,最少要爬多少10cm.(不计杯壁厚度与小虫的尺寸)
圆柱形玻璃杯高8cm,杯口周长为12cm,内壁距杯口2cm的点A处有一点蜜糖.A点正对面的外壁(不是A点的外壁)距杯底2cm的点B处有一小虫.若小虫沿杯壁爬向蜜糖饱食一顿,最少要爬多少10cm.(不计杯壁厚度与小虫的尺寸)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?平面a,b?平面β且α∩β=∅ | B. | a?平面α,b?平面α | ||
| C. | a?平面α,b?平面β | D. | a∩b=∅且a不平行于b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
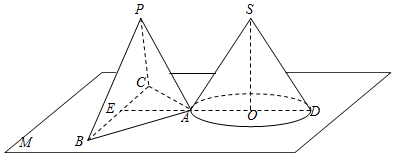
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com