Question

7．如果函数f（x）=$\frac{1}{2}$（m-2）x²+（n-8）x+1（m≥0，n≥0）在区间[1，2]上单调递减，则3m+2n的最大值为22．

Answer 1

分析 根据函数单调性的性质结合一元二次函数的对称性和单调区间的关系建立不等式，利用线性规划进行求解即可．

解答 解：当m=2时，f（x）=（n-8）x+1，在区间[1，2]上单调递减，n-8＜0，
0≤n＜8，
∴3m+2n＜22；
当m≠2时，抛物线的对称轴为x=-$\frac{n-8}{m-2}$，
当m＞2时，-$\frac{n-8}{m-2}$≥2，即2m+n≤12．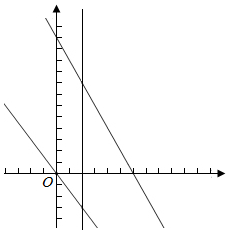

由函数图象可知当过点（2，8）时，z取最大值，z＜22；
当m＜2，抛物线开口向下，据题意得，-$\frac{n-8}{m-2}$≤1，
m+n≥10，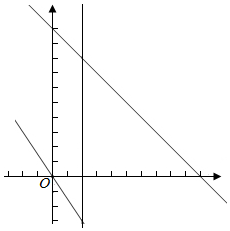

由函数图象可知当过点（2，8）时，z＜22，
故答案为：22

点评 本题主要考查一元二次函数性质的应用，根据函数单调性和对称轴之间的关系是解决本题的关键．注意要进行分类讨论，属于中档题．