
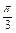 ,△ABC是等边三角形
,△ABC是等边三角形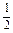 或cosB=
或cosB=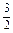 (舍去).∴cosB=
(舍去).∴cosB=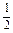 .
. ,∴B=
,∴B=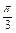 .
. =
= =
=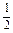 ,
,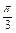 ,∴△ABC是等边三角形.
,∴△ABC是等边三角形.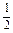 或cosB=
或cosB=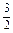 (舍去).
(舍去).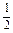 ,∵0<B<
,∵0<B< ,∴B=
,∴B=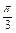 ,
,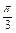 =
=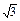 .
.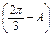 =
=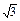 ,
, -cos
-cos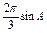 =
=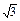 .
.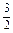 sinA+
sinA+ cosA=
cosA=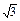 ,∴sin
,∴sin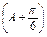 =1.
=1.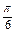 =
=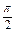 ,∴A=
,∴A=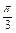 ,
,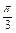 ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.

科目:高中数学 来源:不详 题型:解答题
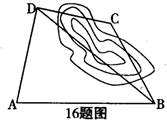 如图,为了计算渭河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据:
如图,为了计算渭河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据: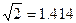 ,
,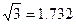 ,
,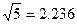 .)
.)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 -sinA,cosA),若|m+n|=2.
-sinA,cosA),若|m+n|=2. ,且c=
,且c= a,求△ABC的面积.
a,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
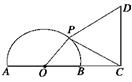 的延长线上,BC=1,点P为半圆上的一个动点,以
的延长线上,BC=1,点P为半圆上的一个动点,以查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com