
分析 (1)设出参赛人数的分数,根据分数符合正态分布,根据成绩在90分以上(含90分)的学生有13名,列出大于90分的学生的概率,成绩在90分以上(含90分)的学生人数约占全体参赛人数的0.0013,列出比例式,得到参赛的总人数.
(2)设受奖的学生的分数线为x0.由P(X≥x0)=$\frac{228}{10000}$=0.0228<0.5,可得x0>60.进一步得知P(120-x0<X<x0)=1-2P(X≥x0)=0.9544,即可得x0=60+20=80,故受奖学生的分数线是80.
解答 解:(1)设学生的成绩为X,共有n人参加竞赛,
∵X~N(60,100),∴μ=60,σ=10.
∴P(X≥90)=$\frac{1}{2}$•[1-P(30<X<90)]=$\frac{1}{2}•$(1-0.9974)=0.0013.
又P(X≥90)=$\frac{13}{n}$,∴$\frac{13}{n}$=0.0013.∴n=10000.
故此次参加竞赛的学生总数共有10000人.
(2)设受奖的学生的分数线为x0.则P(X≥x0)=$\frac{228}{10000}$=0.0228.
∵0.0228<0.5,∴x0>60.∴P(120-x0<X<x0)=1-2P(X≥x0)=0.9544,
∴x0=60+20=80.
故受奖学生的分数线是80.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,考查标准正态分布表的应用,考查学生的计算能力,是一个实际应用问题.


科目:高中数学 来源: 题型:解答题
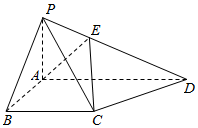 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{7}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [-$\frac{π}{4}$,-$\frac{π}{8}$] | C. | [-$\frac{π}{4}$,$\frac{π}{8}$] | D. | [-$\frac{π}{8}$,$\frac{π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2016}$ | B. | $\frac{1}{2016}$ | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com