
分析 根据条件画出图形,并取AB中点E,连接CE,从而得出四边形ADCE为平行四边形,进而得出$\overrightarrow{DC}=\frac{1}{2}\overrightarrow{AB}$,进行数量积的运算即可求出$\overrightarrow{AB}•\overrightarrow{DC}$的值.
解答 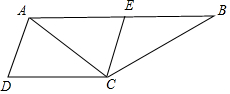 解:如图,取AB的中点E,连接CE,则:
解:如图,取AB的中点E,连接CE,则:
$\overrightarrow{CE}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$;
∴$\overrightarrow{DA}=\overrightarrow{CE}$;
∴四边形ADCE是平行四边形;
∴$\overrightarrow{DC}=\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}$,且AB=2;
∴$\overrightarrow{AB}•\overrightarrow{DC}=\frac{1}{2}{\overrightarrow{AB}}^{2}=2$.
故答案为:2.
点评 考查向量加法的平行四边形法则,向量相等的概念,平行四边形的概念,向量数乘的几何意义,数量积的运算.


科目:高中数学 来源: 题型:选择题
| A. | 若f(x)是奇函数,则f(x)是单调函数 | |
| B. | 命题“若x2-x-2=0,则x=1”的逆否命题是“若x≠1,则x2-x-2=0” | |
| C. | 命题p:?x∈R,2x>1024,则¬p:?x0∈R,${2^{x_0}}<1024$ | |
| D. | 命题“?x∈(-∞,0),2x<x2”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
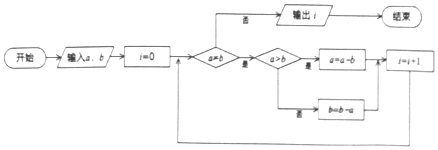
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com