
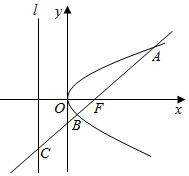
 如图,过抛物线y2=2px(p>0)的焦点F的直线l依次交抛物线及其准线与点A,B,C,若BC|=2|BF|,且|AF|=3,则抛物线的方程是y2=3x.
如图,过抛物线y2=2px(p>0)的焦点F的直线l依次交抛物线及其准线与点A,B,C,若BC|=2|BF|,且|AF|=3,则抛物线的方程是y2=3x. 分析 分别过点A,B作准线的垂线,分别交准线于点E,D,则BD=BF,故∠BCD=30°,于是AC=2AE,从而得出BD,利用△BCD∽△FCG得出p,从而得出抛物线方程.
解答 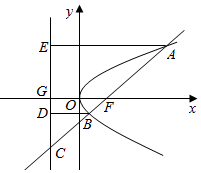 解:分别过点A,B作准线的垂线,分别交准线于点E,D,
解:分别过点A,B作准线的垂线,分别交准线于点E,D,
设|BF|=a,则|BC|=2a,|BD|=a,∴∠BCD=30°,
在直角三角形ACE中,∵|AF|=3,|AC|=3+3a,
∴2|AE|=|AC|
∴3+3a=6,即a=1,
∵BD∥FG,
∴$\frac{1}{p}$=$\frac{2}{3}$,解得p=$\frac{3}{2}$,
∴抛物线方程为y2=3x.
故答案为:y2=3x.
点评 本题主要考查了抛物线的性质.考查了学生对抛物线的定义和基本知识的综合把握.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | 存在唯一平面α,使得a?α,且b∥α | B. | 存在唯一直线l,使得l∥a,且l⊥b | ||
| C. | 存在唯一直线l,使得l⊥a,且l⊥b | D. | 存在唯一平面α,使得a?α,且b⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
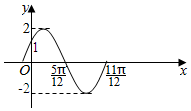 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,0) | B. | (5,0) | C. | (3,2) | D. | (5,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a>4a | B. | 2lga<lga | C. | a2+|a|≤0 | D. | |a+$\frac{1}{a}}$|<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com