
分析 (1)移项通分,整理化简分式不等式,利用穿根法求解集;
(2)|x-1|+|x+2|的几何意义解答.
解答 解:(1)$x-\frac{4}{x-1}<1$,移项通分得$\frac{{x}^{2}-2x-3}{x-1}<0$,即$\frac{(x-3)(x+1)}{x-1}<0$,如图,由穿根法得到不等式的解集为(-∞,-1)∪(1,3);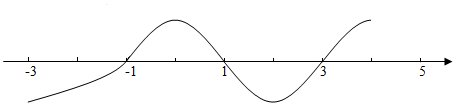
(2)|x-1|+|x+2|>4,根据|x-1|+|x+2|表示数轴上点到1与2的距离和,所以当x∈$(-\frac{5}{2},\frac{3}{2})$时,|x-1|+|x+2|≤4,不满足题意,所以|x-1|+|x+2|>4的x范围是(-∞,$-\frac{5}{2}$)∪($\frac{3}{2}$,+∞).
点评 本题考查了分式不等式和绝对值不等式的解法;注意:分式不等式在不知道分母符号的前提下,不能去分母,只能移项通分,然后解之;如果可以分解成多个一次因式积的形式,可以利用穿根法求不等式的解集;绝对值不等式的解法可以通过讨论去绝对值;如果几何意义明显的,可以利用几何意义解之.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相离 | C. | 相交但不过圆心 | D. | 相交且过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
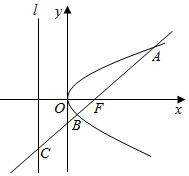 如图,过抛物线y2=2px(p>0)的焦点F的直线l依次交抛物线及其准线与点A,B,C,若BC|=2|BF|,且|AF|=3,则抛物线的方程是y2=3x.
如图,过抛物线y2=2px(p>0)的焦点F的直线l依次交抛物线及其准线与点A,B,C,若BC|=2|BF|,且|AF|=3,则抛物线的方程是y2=3x.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com