
| A. | (3,0) | B. | (5,0) | C. | (3,2) | D. | (5,4) |
分析 确定抛物线的方程,由|AF|+|BF|=8,利用抛物线的定义转化为x1+x2+2=8,从而求出A,B两点横坐标的和,设出C的坐标,利用C在AB的垂直平分线上得|AC|=|BC|,代入两点间的距离公式后移向整理,代入两横坐标的和后可求m的值.
解答 解:设A(x1,y1),B(x2,y2)(x1≠x2),
∵点M(-1,-2)是抛物线y2=2px(p>0)的准线上一点,
∴抛物线方程为y2=4x,其准线x=1.
∵|AF|+|BF|=8,
∴由定义得x1+x2+2=8,则x1+x2=6.
设直线AB的垂直平分线l与x轴的交点C(m,0).
由C在AB的垂直平分线上,从而|AC|=|BC|,
即(x1-m)2+y12=(x2-m)2+y22,
即(x1+x2-2m)(x1-x2)=4x2-4x1=-4(x1-x2),
∵x1≠x2,∴x1+x2-2m=-4.
又∵x1+x2=6,∴m=5,
∴点C的坐标为(5,0).
即直线AB的垂直平分线l与x轴的交点为定点(5,0).
故选:B.
点评 本题主要考查抛物线的定义和方程,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,这也是高考常考的知识点,属中档题.


科目:高中数学 来源: 题型:填空题
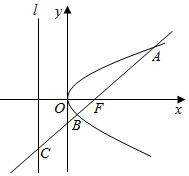 如图,过抛物线y2=2px(p>0)的焦点F的直线l依次交抛物线及其准线与点A,B,C,若BC|=2|BF|,且|AF|=3,则抛物线的方程是y2=3x.
如图,过抛物线y2=2px(p>0)的焦点F的直线l依次交抛物线及其准线与点A,B,C,若BC|=2|BF|,且|AF|=3,则抛物线的方程是y2=3x.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂直 | B. | 共线 | C. | 不垂直 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com