
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| B. | 对于命题p:?x0∈R,x${\;}_{0}^{2}$+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn”是“em<en”的充分不必要条件 | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
分析 A利用逆否命题的定义判断即可;
B存在命题,应把存在改为任意,再否定结论;
C根据充分不必要条件的定义判断即可;
D根据且命题的真假判断依据判断即可.
解答 解:对于A,逆否命题把命题的条件和结论互换,再同时否定,故命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”,故正确;
对于B,对于存在命题,应把存在改为任意,再否定结论,故命题p:?x0∈R,x${\;}_{0}^{2}$+x0+1<0,则¬p:?x∈R,x2+x+1≥0,故正确;
对于C,若m,n∈R,“lnm<lnn”,则0<m<n,可得“em<en”,但由“em<en”,m,n也可能为负值,不一定得出lnm<lnn”,故应是充分不必要条件,故正确;
对于D,且命题为假命题,p和q不能都是真命题,但也不一定都是假命题,故错误.
故选:D.
点评 考查了四中命题间的逻辑关系,属于常规题型,应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
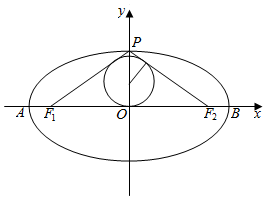 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
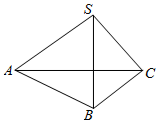 如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:
如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com