
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
分析 可设F1P=m,F2P=n,F1F2=2c,由余弦定理便得到4c2=m2+n2-mn,设a1是椭圆的长半轴,a1是双曲线的实半轴,由椭圆及双曲线定义即可得到m+n=2a1,m-n=2a1,从而可以求出m,n.再根据离心率互为倒数便可得到c2=a1a2,将m,n及c2都带入上式便可得出a1=3a2,从而有$\frac{c}{{a}_{1}}•\frac{3c}{{a}_{1}}=1$,这样便可求出椭圆的离心率.
解答 解:设F1P=m,F2P=n,F1F2=2c;
由余弦定理得,(2c)2=m2+n2-2mncos60°,即4c2=m2+n2-mn;
设a1是椭圆的长半轴,a2是双曲线的实半轴;
由椭圆及双曲线定义,得m+n=2a1,m-n=2a2;
∴m=a1+a2,n=a1-a2,将它们代入前式得3a22-4c2+a12=0;
∵离心率互为倒数;
∴$\frac{c}{{a}_{1}}=\frac{{a}_{2}}{c}$,∴c2=a1a2;
∴$3{{a}_{2}}^{2}-4{a}_{1}{a}_{2}+{{a}_{1}}^{2}=(3{a}_{2}-{a}_{1})$(a2-a1)=0;
根据题意,a2≠a1,∴a1=3a2;
∴e1•e2=$\frac{c}{{a}_{1}}•\frac{c}{{a}_{2}}=\frac{c}{{a}_{1}}•\frac{3c}{{a}_{1}}=1$
即3e12=1;
∴e1=$\frac{\sqrt{3}}{3}$.
故选:A.
点评 考查余弦定理,椭圆和双曲线的焦点及离心率,离心率的计算公式,椭圆的长半轴,双曲线的实半轴,以及椭圆和双曲线的定义.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\sqrt{2}-1$) | B. | [$\sqrt{2}-1,\frac{1}{2}$] | C. | [$\frac{1}{2},\frac{\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{2}}{2},1$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
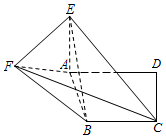 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | n<2016? | B. | n≤2016? | C. | n>2016? | D. | n≥2016? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| B. | 对于命题p:?x0∈R,x${\;}_{0}^{2}$+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn”是“em<en”的充分不必要条件 | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com