
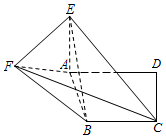
 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.分析 (I)作 FG∥EA,AG∥EF,连结EG交AF于H,连结BH,BG,由题设条件推导出四边形AEFG为正方形,从而得到CDAG为平行四边形,由此能够证明CE∥面ABF.
(Ⅱ)以A为原点,AG为x轴,AD为y轴,AE为z轴,建立空间直角坐标系A-xyz.利用向量法能够求出结果.
解答 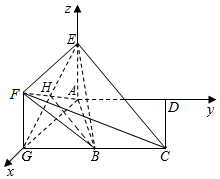 (I)证明:如图,作 FG∥EA,AG∥EF,
(I)证明:如图,作 FG∥EA,AG∥EF,
连结EG交AF于H,连结BH,BG,
∵EF∥CD且EF=CD,
∴AG∥CD,即点G在平面ABCD内
由AE⊥平面ABCD,知AE⊥AG,
∴四边形AEFG为正方形,
∴CDAG为平行四边形,…(2分)
∴H为EG的中点,B为CG中点,∴BH∥CE,
∴CE∥面ABF.…(4分)
(Ⅱ)解:如图,以A为原点,AG为x轴,AE为z轴,AD为y轴,
建立空间直角坐标系A-xyz.
由题意得:A(0,0,0),G(1,0,0),E(0,0,1),D(0,2,0),C(1,2,0)
设M(1,y0,0),则$\overrightarrow{ED}=(0\;,\;\;2\;,\;\;-1)$,$\overrightarrow{DM}=(1,{y_0}-2,0)$,
设面EMD的一个法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{ED}=2y-z=0}\\{\overrightarrow{n}•\overrightarrow{DM}=x+({y}_{0}-2)y=0}\end{array}\right.$,令y=1,得z=2,x=2-y0,
∴$\overrightarrow{n}$=(2-y0,1,2).…(8分)
又∵$\overrightarrow{AE}⊥面\;AMD$,
∴$\overrightarrow{AE}=(0,\;\;0,\;\;1)$为面AMD的法向量,
∵二面角E-MD-A的大小为$\frac{π}{3}$,
∴|cos<$\overrightarrow{n},\overrightarrow{AE}$>|=|$\frac{2}{1×\sqrt{(2-{{y}_{0})}^{2}+1+4}}$|=cos$\frac{π}{3}$=$\frac{1}{2}$,
解得即$\sqrt{(2-{y}_{0})^{2}+5}$=4,
平方得(2-y0)2+5=16,
即(2-y0)2=9,得y0=-1(舍)或y0=3.
∴在BC上存在点M,且|CM|=5-2=3,…(12分)
点评 本题考查直线与平面垂直的证明以及二面角的应用,考查直线与直线垂直的证明,考查满足条件的点是否存在的判断,解题时要注意向量法的合理运用.利用向量法是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
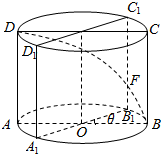 如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.
如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
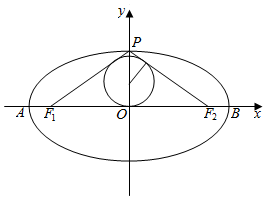 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com