
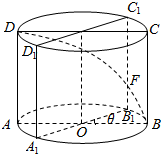
 ��ͼ��ʾ����֪Բ��OO1�ĵ���뾶��2������4��ABCD��Բ����һ������棬����E��B�����������Բ���IJ��浽���D�����侭����·�����ʱ���ڲ������µ�������S���������ABCD������OO1��ʱ����ת�ȣ�0���ȣ��У���B1C1������S���ڵ�F��
��ͼ��ʾ����֪Բ��OO1�ĵ���뾶��2������4��ABCD��Բ����һ������棬����E��B�����������Բ���IJ��浽���D�����侭����·�����ʱ���ڲ������µ�������S���������ABCD������OO1��ʱ����ת�ȣ�0���ȣ��У���B1C1������S���ڵ�F������ ��2������=$\frac{��}{2}$ʱ����B1ǡ��ΪAB���е㣬����FΪB1C1�е㣬��������ƽ�е��ж���������֤�����ɣ�
��3�����ݶ���ǵĶ������������D-AB-F��ƽ��ǣ����������εı߽ǹ�ϵ������⼴�ɣ�
��� �⣺��1������=$\frac{��}{2}$ʱ����B1ǡ��Ϊ��AB���е㣬
��FΪB1C1�е㣬
ȡD1A1���е�G��
��GC1��FA1��
��C1G?ƽ��A1BF��A1F?ƽ��A1BF��
��C1G��ƽ��A1BF��
��2������=$\frac{��}{3}$ʱ��$\widehat{B{B}_{1}}$=$\frac{��}{3}��2$=$\frac{2��}{3}$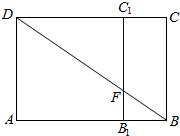
���������չ����ͼ��
��AB=4��AD=4��
��$\frac{{B}_{1}F}{AD}=\frac{B{B}_{1}}{AB}$��
��B1F=$\frac{B{B}_{1}•AD}{AB}$=$\frac{\frac{��}{3}��4}{4��}$=$\frac{1}{3}$��
�߶����D-AB-B1Ϊֱ����ǣ�
��B1��B1Q��AB��Q������FQ��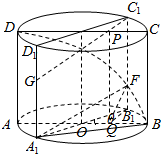
����B1Q��AB��B1F��AB��
��AB��ƽ��B1FQ��
��AB��PQ��
���ǡ�FQB1��Ϊ�����D-AB-F��ƽ��ǵ���ǣ���PQB1��Ϊ�����D-AB-F��ƽ��ǣ�
���PQB1=$\frac{��}{2}$-��FQB1������FQB1=$\frac{��}{2}$-��PQB1��
QB1=OB1sin$\frac{��}{3}$=2��$\frac{\sqrt{3}}{2}$=$\sqrt{3}$��
��QF=$\sqrt{{B}_{1}{F}^{2}+Q{{B}_{1}}^{2}}$=$\sqrt{��\frac{1}{3}��^{2}+��\sqrt{3}��^{2}}$=$\sqrt{\frac{1}{9}+3}$=$\frac{2\sqrt{7}}{3}$��
��Rt��FB1Q��sin��FQB1=sin��$\frac{��}{2}$-��PQB1��=cos��PQB1��
��sin��FQB1=$\frac{{B}_{1}F}{QF}$=$\frac{\frac{1}{3}}{\frac{2\sqrt{7}}{3}}$=$\frac{\sqrt{7}}{14}$��
��cos��PQB1=sin��FQB1=$\frac{\sqrt{7}}{14}$��
�������D-AB-F������ֵΪ$\frac{\sqrt{7}}{14}$��
���� ���⿼��ֱ�ߺ�ƽ��ƽ�е��жϣ�����ǵ���⣬��������ƽ�е��ж������Լ�����ǵ�ƽ��ǵĶ�����������ǵ�ƽ����ǽ������Ĺؼ�������ѧ��������������������


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
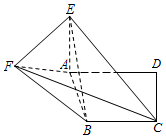 ��ͼ����ֱ������ABCD�У�AD��BC����ADC=90�㣬AE��ƽ��ABCD��EF��CD��BC=CD=AE=EF=$\frac{1}{2}$AD=1��
��ͼ����ֱ������ABCD�У�AD��BC����ADC=90�㣬AE��ƽ��ABCD��EF��CD��BC=CD=AE=EF=$\frac{1}{2}$AD=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
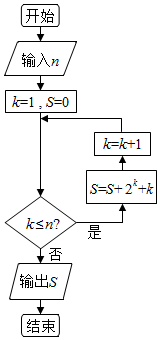
| A�� | 20 | B�� | 40 | C�� | 77 | D�� | 546 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | l | C�� | i | D�� | -i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{5}$ | B�� | $-\frac{1}{5}i$ | C�� | $\frac{1}{5}$ | D�� | $\frac{1}{5}i$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com