
分析 (1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),先求出c=$\sqrt{2}$,由椭圆过点($\sqrt{2}$,1),得$\frac{2}{{a}^{2}}+\frac{1}{{b}^{2}}$=1,由此能求出椭圆的标准方程.
(2)由$\overrightarrow{AP}=2\overrightarrow{PB}$,得$\left\{\begin{array}{l}{-{x}_{1}=2{x}_{2}}\\{1-{y}_{1}=2({y}_{2}-1)}\end{array}\right.$,设直线方程为y=kx+1,代入椭圆,得(2k2+1)x2+4kx-2=0,由此利用韦达定理,结合已知条件能求出△AOB的面积.
解答 解:(1)∵对称中心在原点的椭圆的一个焦点与圆x2+y2-2$\sqrt{2}$x=0的圆心重合,且椭圆过点($\sqrt{2}$,1),
∴设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为半焦距,c=$\sqrt{2}$,
∴a2-b2=2,①
由椭圆过点($\sqrt{2}$,1),得$\frac{2}{{a}^{2}}+\frac{1}{{b}^{2}}$=1,②
由①②,得a2=4,b2=2,
∴所求椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
(2)设A(x1,y1),B(x2,y2),由$\overrightarrow{AP}=2\overrightarrow{PB}$,得$\left\{\begin{array}{l}{-{x}_{1}=2{x}_{2}}\\{1-{y}_{1}=2({y}_{2}-1)}\end{array}\right.$,
设直线方程为y=kx+1,代入椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,得(2k2+1)x2+4kx-2=0,
解得x=$\frac{-2k±\sqrt{8{k}^{2}+2}}{2{k}^{2}+1}$,设${x}_{1}=\frac{-2k-\sqrt{8{k}^{2}+2}}{2{k}^{2}+1}$,${x}_{2}=\frac{-2k+\sqrt{8{k}^{2}+2}}{2{k}^{2}+1}$,
则-$\frac{-2k-\sqrt{8{k}^{2}+2}}{2{k}^{2}+1}$=2•$\frac{-2k+\sqrt{8{k}^{2}+2}}{2{k}^{2}+1}$,解得${k}^{2}=\frac{1}{14}$,
∴△AOB的面积S=$\frac{1}{2}$|OP|•|x1-x2|=$\frac{1}{2}$•$\frac{2\sqrt{8{k}^{2}+2}}{2{k}^{2}+1}$=$\frac{\sqrt{126}}{8}$=$\frac{3\sqrt{14}}{8}$.
点评 本题考查椭圆方程的求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、向量的数量积的合理运用.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,1) | C. | (2,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B. | $\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$ | C. | $\frac{{x}^{2}}{5}+\frac{{y}^{2}}{3}=1$ | D. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
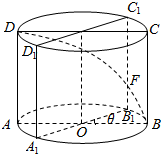 如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.
如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com