
分析 ①抽样是间隔相同,故①应是系统抽样;
②根据相关系数的公式可判断;
③由回归方程的定义可判断;
④k越小,“X与Y有关系”的把握程度越小.
解答 解:根据抽样是间隔相同,且样本间无明显差异,故①应是系统抽样,即①为假命题;
两个随机变量相关性越强,则相关系数的绝对值越接近于1;两个随机变量相关性越弱,则相关系数的绝对值越接近于0;故②为真命题;
在回归直线方程$\widehat{y}$=0.4x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.4个单位,故③为真命题;
对分类变量X与Y的随机变量K2的观侧值k来说,k越小,“X与Y有关系”的把握程度越小,故④为假命题;
故答案为:②③.
点评 考查了系统抽样的概念和相关系数,回归方程定义的考查,属于基础题型,应理解.


科目:高中数学 来源: 题型:解答题
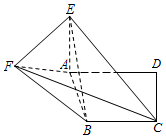 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
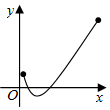
| A. | f(x)=2x+lgx+2 | B. | f(x)=2x+lgx-2 | C. | f(x)=2x-lgx+2 | D. | f(x)=2x-lgx-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | $\frac{2\sqrt{3}}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3或-1 | B. | 9或1 | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com