练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知曲线C的参数方程为$\left\{\begin{array}{l}x=2cosα\\ y=1+2sinα\end{array}\right.$（α为参数），直线l的参 数方程为$\left\{\begin{array}{l}x=1+tcos45°\\ y=tsin45°\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．
    （Ⅰ）求曲线C的极坐标方程；
    （Ⅱ）求直线l截曲线C所得的弦长．

    分析 （I）将曲线C的参数方程化为直角坐标方程，再转化为极坐标方程；
    （II）将l的参数方程代入曲线C的普通方程解出参数，利用参数的几何意义得出弦长．

    解答 解：（Ⅰ）曲线C的参数方程化为直角坐标方程为x2+（y-1）2=4．
    令x=ρcosθ，y=ρsinθ代入上式，
    得曲线C的极坐标方程为：ρ2-2ρsinθ-3=0．
    （Ⅱ）将 $\left\{\begin{array}{l}x=1+tcos45°\\ y=tsin45°\end{array}\right.$代入x2+（y-1）2=4得t2=2，∴${t_1}=\sqrt{2}，{t_2}=-\sqrt{2}$，
    所以所求弦长为$|{{t_2}-{t_1}}|=2\sqrt{2}$．

    点评 本题考查了参数方程，极坐标方程与普通方程的转化，参数方程的应用，属于基础题；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．设F1、F2分别是椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1的左、右焦点，P为椭圆上任一点，点M的坐标为（6，4），则|PM|+|PF1|的最大值为（　　）
    A．13B．14C．15D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）上总存在点P，使$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$，F1、F2为椭圆的焦点，那么椭圆离心率e的取值范围是（　　）
    A．（0，$\sqrt{2}-1$）B．[$\sqrt{2}-1，\frac{1}{2}$]C．[$\frac{1}{2}，\frac{\sqrt{2}}{2}$]D．[$\frac{\sqrt{2}}{2}，1$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

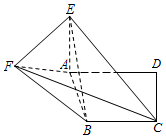    15．如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AE⊥平面ABCD，EF∥CD，BC=CD=AE=EF=$\frac{1}{2}$AD=1．
    （1）求证：CE∥平面ABF；
    （2）在直线BC上是否存在点M，使二面角E-MD-A的大小为$\frac{π}{3}$？若存在，求出CM的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．要计算$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2016}$的结果，下面的程序框图中的横线上可以填（　　）
    A．n＜2016？B．n≤2016？C．n＞2016？D．n≥2016？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知z=$\frac{2+i}{1-2i}$（i为虚数单位），则复数z=（　　）
    A．-1B．lC．iD．-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下列说法错误的是（　　）
    A．命题“若x2-3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2-3x+2≠0”
    B．对于命题p：?x0∈R，x${\;}_{0}^{2}$+x0+1＜0，则￢p：?x∈R，x2+x+1≥0
    C．若m，n∈R，“lnm＜lnn”是“em＜en”的充分不必要条件
    D．若p∧q为假命题，则p、q均为假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．函数f（x）的部分图象如图所示，则f（x）的解析式可以是（　　）
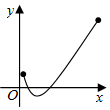
    A．f（x）=2x+lgx+2B．f（x）=2x+lgx-2C．f（x）=2x-lgx+2D．f（x）=2x-lgx-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在正项等比数列{an}中，若3a1，$\frac{1}{2}$a3，2a2成等差数列，则$\frac{{a}_{2016}-{a}_{2017}}{{a}_{2014}-{a}_{2015}}$=（　　）
    A．3或-1B．9或1C．3D．9

    查看答案和解析>>

    同步练习册答案