
分析 利用$ρ=\sqrt{{x}^{2}+{y}^{2}}$,tanθ=$\frac{y}{x}$,-π≤θ<π,点M在第四象限,即可得出.
解答 解:点M的直角坐标是$(1,-\sqrt{3})$,
∴$ρ=\sqrt{{1}^{2}+(-\sqrt{3})^{2}}$=2,tanθ=$\frac{-\sqrt{3}}{1}$=-$\sqrt{3}$,∵-π≤θ<π,点M在第四象限,
∴θ=-$\frac{π}{3}$,
则点M的极坐标为$(2,-\frac{π}{3})$.
故答案为:$(2,-\frac{π}{3})$.
点评 本题考查了极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③④ | C. | ③④ | D. | ①②⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 79 | 74 | 88 | 97 | 90 | 82 |
| 乙 | 74 | 77 | 81 | 92 | 96 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
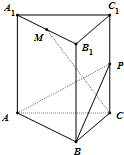 如图,直三棱柱ABC-A1B1C1的底面是边长为4正三角形,$A{A_1}=2\sqrt{6}$,M为A1B1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为4正三角形,$A{A_1}=2\sqrt{6}$,M为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com