
分析 (Ⅰ)直接把已知点的坐标代入数f(x)=x2+ax+b,得到关于a,b的方程组,求解得到a,b的值,则f(x)的解析式可求;
(Ⅱ)写出二次函数的对称轴方程,由题意可得1<$-\frac{a}{2}$<2,则实数a的取值范围可求.
解答 解:(Ⅰ)由题意得$\left\{\begin{array}{l}{a+b+1=4}\\{2a+b+4=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{b=5}\end{array}\right.$.
∴f(x)=x2-2x+5;
(Ⅱ)函数f(x)=x2+ax+b的对称轴方程为x=-$\frac{a}{2}$,
∵f(x)的区间[1,2]不单调,
∴1<$-\frac{a}{2}$<2,即-4<a<-2.
∴实数a的取值范围是(-4,-2).
点评 本题考查利用待定系数法求函数的解析式,考查二次函数的性质,是基础题.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,10,15 | B. | 3,9,18 | C. | 5,9,16 | D. | 3,10,17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$•|$\overrightarrow{a}$|=$\overrightarrow{a}$2 | B. | ($\overrightarrow{a}$•$\overrightarrow{b}$)2=$\overrightarrow{a}$2•$\overrightarrow{b}$2 | C. | ($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}$•$\overrightarrow{c}$) | D. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
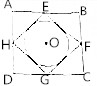 已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.
已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com