
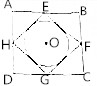
 已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.
已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$. 分析 由题意ABCD是正方形,设其边长为a,则${S}_{正方形ABCD}={a}^{2}$,推导出EFGH是边长为$\frac{\sqrt{2}}{2}$a,从而圆O的半径r=$\frac{\sqrt{2}}{4}a$,在正方形ABCD内投一点,由几何概型得该点落在圆O内的概率p=$\frac{{S}_{圆O}}{{S}_{正方形ABCD}}$,由此能求结果.
解答 解:由题意ABCD是正方形,设其边长为a,则${S}_{正方形ABCD}={a}^{2}$,
∵E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,
∴EFGH是边长为$\frac{\sqrt{2}}{2}$a,∴圆O的半径r=$\frac{\sqrt{2}}{4}a$,
∴S圆O=$π{r}^{2}=π×\frac{2}{16}{a}^{2}=\frac{π{a}^{2}}{8}$,
∴在正方形ABCD内投一点,该点落在圆O内的概率:
p=$\frac{{S}_{圆O}}{{S}_{正方形ABCD}}$=$\frac{\frac{π{a}^{2}}{8}}{{a}^{2}}$=$\frac{π}{8}$.
故答案为:$\frac{π}{8}$.
点评 本题考查概率的求法,涉及到正方形内切圆、几何概型等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | M=P | B. | P?M | C. | M?P | D. | (∁UM)∩P=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{2}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com