练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知角A是△ABC的一个内角，若sin A+cos A=$\frac{3}{5}$，则sinA-cosA等于$\frac{{\sqrt{41}}}{5}$．

    分析 利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得sinA-cosA的值．

    解答 解：∵角A是△ABC的一个内角，若sin A+cos A=$\frac{3}{5}$，
    ∴1+2sinAcosA=$\frac{9}{25}$，∴sinAcosA=-$\frac{8}{25}$，∴A为钝角，
    则sinA-cosA=$\sqrt{{（sinA-cosA）}^{2}}$=$\sqrt{1-2sinAcosA}$=$\sqrt{1-2•（-\frac{8}{25}）}$=$\frac{\sqrt{41}}{5}$，
    故答案为：$\frac{\sqrt{41}}{5}$．

    点评 本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．已知正项等比数列{an}中，a5a2n-5=102n（n≥3，n∈N*），则当n≥1，n∈N*时表达式lga1+lga2+lga3+…+lgan的值为$\frac{n（n+1）}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，其左、右焦点分别为F1，F2，离心率为$\frac{{\sqrt{6}}}{3}$，点R的坐标为$（2\sqrt{2}，\sqrt{6}）$，又点F2在线段RF1的中垂线上．
    （1）求椭圆C的方程；
    （2）设椭圆C的左、右顶点分别为A1，A2，点P在直线$x=-2\sqrt{3}$上（点P不在x轴上），直线PA1，PA2与椭圆C分别交于不同的两点M，N，线段MN的中点为Q，若|MN|=λ|A1Q|，求λ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设bn=（2n+1）2n，Tn是数列{bn}的前n项和，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．某企业共有职工150人，其中高级职称15人，中级职称45人，初级职称90人，现用分层抽样方法抽取一个容量为30的样本，则各职称中抽取的人数分别为（　　）
    A．5，10，15B．3，9，18C．5，9，16D．3，10，17

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an}的前n项和为Sn，a1=1，an≠0，anan+1=4Sn-1．
    （1）求{an}的通项公式；
    （2）若数列{bn}满足$\frac{{a}_{n}}{{b}_{n}}$=2n-1（n∈N*），设Tn是数列{bn}的前n项和，证明Tn＜6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．$\overrightarrow{a}$，$\overrightarrow{b}$都为向量，则下列式子正确的是（　　）
    A．$\overrightarrow{a}$•|$\overrightarrow{a}$|=$\overrightarrow{a}$2B．（$\overrightarrow{a}$•$\overrightarrow{b}$）2=$\overrightarrow{a}$2•$\overrightarrow{b}$2C．（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）D．|$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$|

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

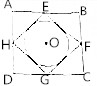    6．已知四边形ABCD中，E，F，G，H分别是线段AB，BC，CD，DA的中点，圆O为四边形EFGH的内切圆，则在正方形ABCD内投一点，该点落在圆O内的概率为$\frac{π}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

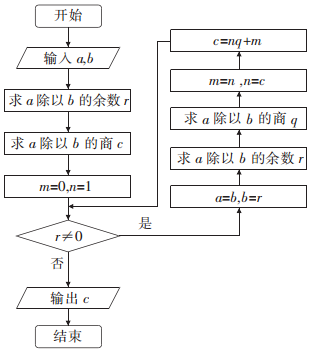
    7．中国古代算书《孙子算经》中有一著名的问题：今有物，不知其数．三三数之剩二；五五数之剩三；七七数之剩二．问物几何？后来，南宋数学家秦九昭在其《数书九章》中对此问题的解法做了系统的论述，并称之为“大衍求一术”．如图程序框图的算法思路源于“大衍求一术”，执行该程序框图，若输入的a，b的值分别为40，34，则输出的c的值为（　　）
    A．7B．9C．20D．22

    查看答案和解析>>

    同步练习册答案