
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{7}{2}$ | C. | 3 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{e},0})$ | B. | (0,+∞) | C. | (0,1) | D. | $[{-\frac{1}{e},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
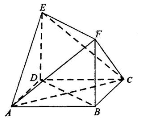 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
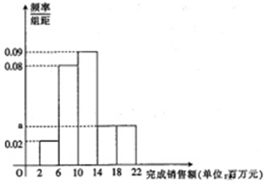 某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.
某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com