Question

1．已知f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的两个极值点分别为x₁，x₂（x₁＜x₂），则a（lnx₁+lnx₂）的取值范围是（　　）

• A． $[{-\frac{1}{e}，0}）$
• B． （0，+∞）
• C． （0，1）
• D． $[{-\frac{1}{e}，+∞}）$

Answer 1

分析 f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的导数f′（x）=$\frac{{e}^{x}（{x}^{2}-2x+a）}{（{x}^{2}+a）^{2}}$，可得方程x²-2x+a=0由两个不等实根，△=4-4a＞0，⇒0＜a＜1．且x₁x₂=a，则a（lnx₁+lnx₂）=alna，（0＜a＜1．），利用导数求值域即可．

解答 解：f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的导数f′（x）=$\frac{{e}^{x}（{x}^{2}-2x+a）}{（{x}^{2}+a）^{2}}$
∵f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的两个极值点分别为x₁，x₂（x₁＜x₂），
∴方程x²-2x+a=0由两个不等实根，△=4-4a＞0，⇒0＜a＜1．
且x₁x₂=a，∴a（lnx₁+lnx₂）=alna，（0＜a＜1．）
令g（a）=alna，（0＜a＜1．），g′（a）=lna+1，
令g′（a）=lna+1=0，得a=$\frac{1}{e}$，
当a$∈（0，\frac{1}{e}$）时，g′（a）=lna+1＜0，a∈（$\frac{1}{e}$，1）时，g′（a）=lna+1＞0，
函数g（a）=alna，（0＜a＜1．）的图象如下：函数g（a）的值域为[-$\frac{1}{e}$，0）．
则a（lnx₁+lnx₂）的取值范围是[-$\frac{1}{e}$，0）．
故选：A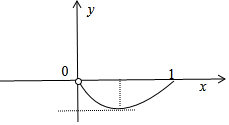

点评 本题考查了函数的极值的概念及存在的充要条件、函数与方程思想，属于中档题．