
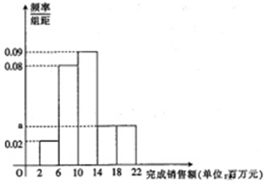
 某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.
某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.分析 (1)根据频率直方图即可求出a的值,
(2)求出各组的人数比,即可求出各组的人数,
(2)求出从这6人中随机抽取2人的情况总数,及两人来自同组的情况数,代入概率公式,可得答案.
解答 解:(1)2a=0.25-(0.02+0.08+0.09),解得a=0.03,
完成完成年度任务的人数200×4×(0.03+0.03)=48人,
(2)这5组的人数比为0.02:0.08:0.09:0.03:0.03=2:8:9:3:3,
故这5组分别应抽取的人数为2,8,9,3,3人
(3)设第四组的4人用a,b,c表示,第5组的3人用A,B,C表示,
从中随机抽取2人的所有情况如下ab,ac,aA,aB,aC,bc,bA,bB,bC,cA,cB,cC,AB,AC,BC共15种,其中在同一组的有ab,ac,bc,AB,AC,BC共6种,
故获得此奖励的2位销售员在同一组的概率$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查的知识点是频率分布直方图,古典概型,难度不大,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
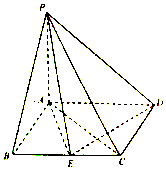 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10$\sqrt{5}$km | B. | 10$\sqrt{7}$km | C. | 10$\sqrt{3}$km | D. | 30km |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)+1 | B. | y=$\frac{1}{2}$sin(2x-$\frac{π}{2}$)+1 | C. | y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$)+1 | D. | y=$\frac{1}{2}$sin($\frac{1}{2}$x-$\frac{π}{4}$)+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com